练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．当（2a+1+2b）（2a-1+2b）=63，a+b=±4．

    分析 将（2a+2b）看作一个整体，然后利用平方差公式进行计算求出（2a+2b）2，再求解即可．

    解答 解：∵（2a+1+2b）（2a-1+2b）
    =[（2a+2b）+1][（2a+2b）-1]
    =（2a+2b）2-1，
    ∴（2a+2b）2-1=63，
    ∴（2a+2b）2=64，
    即4（a+b）2=64，
    ∴（a+b）2=16，
    ∴a+b=±4．
    故答案为：±4．

    点评 本题考查了平方差公式，关键要找相同项和相反项，其结果是相同项的平方减去相反项的平方，本题要注意整体思想的利用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

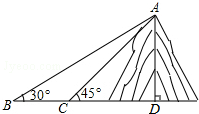    11．如图，小明在一块平地上测山高，先在B处测得山顶A的仰角为30°，然后向山脚直行100米到达C处，再测得山顶A的仰角为45°，求山高AD是多少？（结果保留整数，测角仪忽略不计，参考数据$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．a、b、c三点在数轴上的位置如图所示，化简$\sqrt{{a}^{2}}$-|a+b|+$\sqrt{{b}^{2}-2bc+{c}^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．在数轴上与原点距离2个单位长度的点A和与原点距离$\sqrt{3}$个单位长度的点B之间的距离为2-$\sqrt{3}$或2+$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．已知2a=12，2b=3，求25a÷52b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．设P=a2（-a+b-c），Q=-a（a2-ab+ac），则P与Q的关系是（　　）
    A．P=QB．P＞QC．P＜QD．互为相反数

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．若（am）2=25，an=2，则am-2n=±$\frac{5}{4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知am=4，an=$\frac{1}{2}$，则a2m-3n=128．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．阅读：
    计算：（$\frac{1}{2}$-$\frac{1}{3}$）（2+$\frac{1}{2}$-$\frac{1}{3}$）-（1+$\frac{1}{2}$-$\frac{1}{3}$）2+2
    解：设t=$\frac{1}{2}$-$\frac{1}{3}$，
    则原式=t（t+2）=（1+t）2+2
    =t2+2t-（1+2t+t2）+2
    =1．
    请按照上述的解题思路，解答下列问题：
    计算：（1-ab+2a2）（2a2-ab-1）-（2a2-ab+1）2+2（-a2b+2a3）÷a．

    查看答案和解析>>

    同步练习册答案