
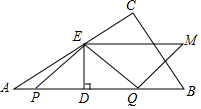
 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm,动点P、Q分别从点A、B同时出发,点P以1cm/s的速度沿A→B向终点B运动.点Q以2cm/s的速度沿B→向终点A运动.过QP的中点D作DE⊥AB交AC于点E.将△PQE绕着EQ的中点旋转180°得到△MEQP.设四边形QMEP的面积为S(cm2),点P运动的时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=3cm,动点P、Q分别从点A、B同时出发,点P以1cm/s的速度沿A→B向终点B运动.点Q以2cm/s的速度沿B→向终点A运动.过QP的中点D作DE⊥AB交AC于点E.将△PQE绕着EQ的中点旋转180°得到△MEQP.设四边形QMEP的面积为S(cm2),点P运动的时间为t(s).分析 (1)如图1中,作CH⊥AB于H,交EM于K.由EM∥AB,推出△CEM∽△CAB,推出$\frac{CK}{CH}$=$\frac{EM}{AB}$,由此构建方程即可解决问题.
(2)分三种情形讨论①当0<t≤1时,如图1中,根据S=PQ•DE即可解决问题.②当1<t≤1.5时,如图2中,根据S=PQ•DE即可解决问题.③如图3中,当1.5<t≤3时,点Q达到终点A,根据S=AP•DE即可解决问题.
(3)分两种情形讨论即可①如图1中,当四边形QMEP是菱形时.②同理如图2中,当四边形QMEP是菱形时.
解答 解:(1)如图1中,作CH⊥AB于H,交EM于K.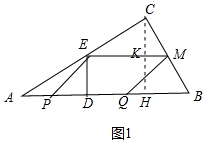
∵AB=3,∠ACB=90°,∠A=30°,
∴BC=$\frac{1}{2}$AB=$\frac{3}{2}$,AC=$\frac{3\sqrt{3}}{2}$,CH=$\frac{1}{2}$AC=$\frac{3\sqrt{3}}{4}$,.
由题意AP=t,BQ=2t,
∴EM=PQ=3-3t,PD=DQ=$\frac{3-3t}{2}$,
∴AD=t+$\frac{3-3t}{2}$=$\frac{3-t}{2}$,
∴DE=$\frac{\sqrt{3}}{3}$AD=$\frac{\sqrt{3}}{6}$(3-t),
∵点M在BC上,EM∥AB,
∴△CEM∽△CAB,
∴$\frac{CK}{CH}$=$\frac{EM}{AB}$,
∴$\frac{\frac{3\sqrt{3}}{4}-\frac{\sqrt{3}}{6}(3-t)}{\frac{3\sqrt{3}}{4}}$=$\frac{3-3t}{3}$,
解得t=$\frac{6}{11}$s.
∴t=$\frac{6}{11}$s时,当点M落在BC边上.
(2)①当0<t≤1时,如图1中,S=PQ•DE=(3-3t)•$\frac{\sqrt{3}}{6}$(3-t)=$\frac{\sqrt{3}}{2}$t2-2$\sqrt{3}$t+$\frac{3\sqrt{3}}{2}$.
②当1<t≤1.5时,如图2中,
由题意,AQ=3-2t,QP=3t-3,DQ=DP=$\frac{3t-3}{2}$,
∴AD=AQ+DQ=3-2t+$\frac{3t-3}{2}$=$\frac{3-t}{2}$,
∴DE=$\frac{\sqrt{3}}{3}$AD=$\frac{\sqrt{3}}{6}$(3-t),
∴S=QP•DE=(3t-3)•$\frac{\sqrt{3}}{6}$(3-t)=-$\frac{\sqrt{3}}{2}$t2+2$\sqrt{3}$t-$\frac{3\sqrt{3}}{2}$.
③如图3中,当1.5<t≤3时,点Q达到终点A,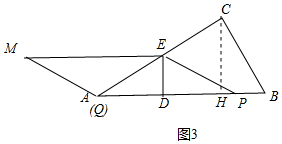
由题意AP=3t-3,AD=$\frac{1}{2}$(3t-3),DE=$\sqrt{3}$AD=$\frac{\sqrt{3}}{2}$(3t-3),
∴S=AP•DE=(3t-3)•$\frac{\sqrt{3}}{2}$(3t-3)=$\frac{9\sqrt{3}}{2}$t2-9$\sqrt{3}$t+$\frac{9\sqrt{3}}{2}$.
综上所述,S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{t}^{2}-2\sqrt{3}t+\frac{3\sqrt{3}}{2}}&{(0<t≤1)}\\{-\frac{\sqrt{3}}{2}{t}^{2}+2\sqrt{3}t-\frac{3\sqrt{3}}{2}}&{(1<t≤1.5)}\\{\frac{9\sqrt{3}}{2}{t}^{2}-9\sqrt{3}t+\frac{9\sqrt{3}}{2}}&{(1.5<t≤3)}\end{array}\right.$.
(3)①如图1中,当四边形QMEP是菱形时,PE=PQ,
∵PD=DQ,
∴PE=2PD,
在Rt△PED中,则有∠PED=30°,
∴DE=$\sqrt{3}$PD,
∴$\frac{\sqrt{3}}{6}$(3-t)=$\sqrt{3}$•$\frac{3-3t}{2}$,
解得t=$\frac{3}{4}$.
②同理如图2中,根据DE=$\sqrt{3}$PD,可得$\frac{\sqrt{3}}{6}$(3-t)=$\sqrt{3}$•$\frac{3t-3}{2}$,
解得t=$\frac{6}{5}$,
综上所述,t=$\frac{3}{4}$s或$\frac{6}{5}$s时,四边形QMEP是菱形.
点评 本题考查四边形综合题、平行四边形的判定和性质、菱形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题.属于中考压轴题.


科目:初中数学 来源: 题型:选择题
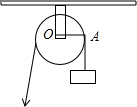 如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )
如图,用一个半径为5cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有摩擦,则重物上升了( )| A. | 5πcm | B. | 3πcm | C. | 2πcm | D. | πcm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
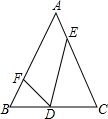 如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )
如图,D、E、F分别是等腰三角形ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=$\frac{3}{2}$,∠FDE=∠B,那么AF的长为( )| A. | 5.5 | B. | 4 | C. | 4.5 | D. | 3.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.
平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
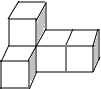 如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )
如图是由5个大小相同的小正方体拼成的几何体,下列说法中,正确的是( )| A. | 主视图是轴对称图形 | B. | 左视图是轴对称图形 | ||
| C. | 俯视图是轴对称图形 | D. | 三个视图都不是轴对称图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com