
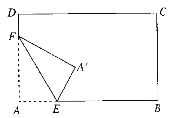
【题目】(1)如图,将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,求∠FEB的度数.
(2)如图,A地和B地都是海上观测站,从A地发现它的北偏东60方向有一艘船P,同时,从B地发现这艘船P在它北偏东30方向.试在图中画出这艘船P的位置.

【答案】(1)120°(2)见解析
【解析】
(1) 根据将长方形纸片的一角作折叠,使顶点A落在A′处,EF为折痕,若EA′恰好平分∠FEB,可以求得∠FEA和∠FEA′、∠BEA′之间的关系,从而可以得到∠FEB的度数.
(2)方位角通常以正北、正南方向为基准线,配以偏东或偏西的角度描述具体的方向,表示两个方向的射线的交点,就是船的位置.
(1)由折叠可知,∠FEA=∠FEA′,
∵EA′平分∠FEB,∴∠FEA′=∠BEA′
∴∠FEA′=∠BEA′=∠FEA .
∵∠FEA′+∠BEA′+∠FEA=180 .
∴3∠FEA′=180 , ∠FEA′=60 .
∴∠FEB=2∠FEA′=120.
(2)画图. 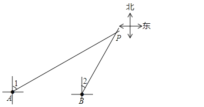


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为![]() 其中
其中![]() .
.
![]() 四边形ABCD的是______
四边形ABCD的是______![]() 填写四边形ABCD的形状
填写四边形ABCD的形状![]()
![]() 当点A的坐标为
当点A的坐标为![]() 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值.
![]() 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线ABCDE描述了一辆汽车在某一直线上行驶过程中,汽车离出发地的距离y(km)和行驶时间x(h)之间的函数关系,根据图中提供的信息,给出下列说法:①汽车共行驶了120km;②汽车在行驶途中停留了0.5h;③汽车在整个行驶过程中的平均速度为![]() km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)
km/h;④汽车自出发后3h~4.5h之间行驶的速度在逐渐减小.其中正确的说法是 .(填上所有正确的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程![]() ﹣1的步骤如下:
﹣1的步骤如下:
(解析)第一步:![]() ﹣1(分数的基本性质)
﹣1(分数的基本性质)
第二步:2x﹣1=3(2x+8)﹣3……(①)
第三步:2x﹣1=6x+24﹣3……(②)
第四步:2x﹣6x=24﹣3+1……(③)
第五步:﹣4x=22(④)
第六步:x=﹣![]() ……(⑤)
……(⑤)
以上解方程第二步到第六步的计算依据有:①去括号法则.②等式性质一.③等式性质二.④合并同类项法则.请选择排序完全正确的一个选项( )
A. ②①③④② B. ②①③④③ C. ③①②④③ D. ③①④②③
查看答案和解析>>
科目:初中数学 来源: 题型:
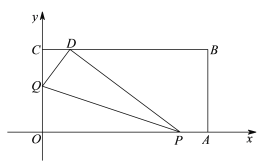
【题目】如图,将一矩形纸片OABC放在平面直角坐标系中,![]() ,
,![]() ,
,![]() .动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动
.动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相同的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
(1)OP =____________, OQ =____________;(用含t的代数式表示)
(2)当![]() 时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
时,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处.
①求点D的坐标;
②如果直线y = kx + b与直线AD平行,那么当直线y = kx + b与四边形PABD有交点时,求b 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】右图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即ABCDCBABC…的方式)从A开始数连续的正整数1,2,3,4…,当数到12时,对应的字母是 ;当字母C第201次出现时,恰好数到的数是 ;当字母C第2n+1次出现时(n为正整数),恰好数到的数是 (用含n的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板放在同一平面内,使直角顶点重合于点O
(1)如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.
(2)如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.
(3)如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
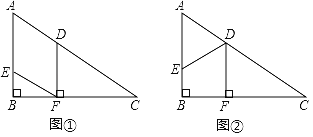
【题目】如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒lcm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.
(I)试用含t的式子表示AE、AD、DF的长;
(Ⅱ)如图①,连接EF,求证:四边形AEFD是平行四边形;
(Ⅲ)如图②,连接DE,当t为何值时,四边形EBFD是矩形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com