
分析 (1)根据题意可以得到相应的方程组,从而可以解答本题;
(2)①根据题意可以得到y与x的函数关系式;
②由题意可知,若不亏本,则所获取利润不小于0,从而可以解答本题.
解答 解:(1)由题意可得,
$\left\{\begin{array}{l}{a+b=40}\\{50a+700=40b}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{a=10}\\{b=30}\end{array}\right.$,
即a,b的值分别是10,30;
(2)①由题意可得,
y=60x+35(40-x)-10×50-30×40=25x-300,
即商店销售完全部草莓所获利润y(元)与x(箱)之间的函数关系式是y=25x-300;
②商店要不亏本,则y≥0,
∴25x-300≥0,
解得,x≥12,
答:当x的值至少为12时,商店才不会亏本.
点评 本题考查二元一次方程组的应用、一次函数的应用、一元一次不等式的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用函数的思想和不等式的性质解答.


科目:初中数学 来源: 题型:解答题
| A组 |  |  |  | |||
| A1 | A2 | A3 | ||||
| B组 |  |  |  |  |  |  |
| B1 | B2 | B3 | B4 | B5 | B6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
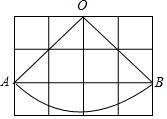 如图,已知小正方形方格的边长为1cm,点O,A,B分别是格点,以O为圆心,OA长为半径作扇形OAB,则弧AB的长为$\sqrt{2}$πcm(结果保留π和根号)
如图,已知小正方形方格的边长为1cm,点O,A,B分别是格点,以O为圆心,OA长为半径作扇形OAB,则弧AB的长为$\sqrt{2}$πcm(结果保留π和根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
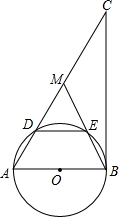 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
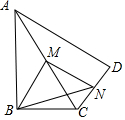 如图,在四边形ABCD中,∠ABC=90°,∠BAD=60°,AC平分∠BAD,AC=AD,M,N分别为AC,CD的中点,AM=1,连接MN,BN,则BN的长为$\sqrt{2}$.
如图,在四边形ABCD中,∠ABC=90°,∠BAD=60°,AC平分∠BAD,AC=AD,M,N分别为AC,CD的中点,AM=1,连接MN,BN,则BN的长为$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
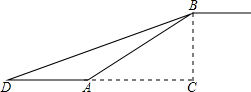 如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).
如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com