
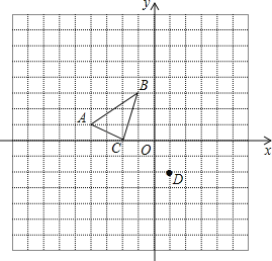
【题目】如图,三角形ABC三个顶点的坐标分别是A(-4,1),B(-1,3),C(-2,0),将三角形ABC平移得到三角形DEF,使点A与点D(1,-2)是对应点.
(1)在图中画出三角形DEF,并写出点B、C的对应点E、F的坐标;
(2)若点P在x轴上,且知三角形PCD的面积等于三角形ABC面积的![]() ,请写出满足条件的点P的坐标.
,请写出满足条件的点P的坐标.
【答案】(1)作图见解析,点E、F的坐标分别为(4,0),(3,3);(2)P点坐标为(1,0),(-5,0).
【解析】
(1)利用点A和点D的坐标特征确定平移的方向和距离,利用此平移规律写出E、F点的坐标,然后描点即可;
(2)设P(m,0),先利用面积的和差求出S△ABC=![]() ,则可得到S△PCD=3,利用三角形面积公式得到
,则可得到S△PCD=3,利用三角形面积公式得到![]() ×2×|m+2|=3,然后求出m即可得到P点坐标.
×2×|m+2|=3,然后求出m即可得到P点坐标.
解:(1)如图,△DEF为所作,由图可得点E、F的坐标分别为(4,0),(3,3);
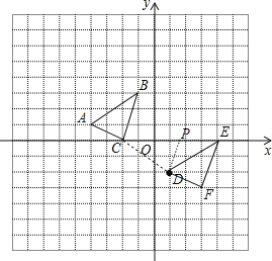
(2)设P(m,0),
S△ABC=3×3-![]() ×2×1-
×2×1-![]() ×3×1-
×3×1-![]() ×3×2=
×3×2=![]() ,
,
∵三角形PCD的面积等于三角形ABC面积的![]() ,
,
∴S△PCD=![]() ×
×![]() =3,
=3,
∴![]() ×2×|m+2|=3,解得m=1或m=-5,
×2×|m+2|=3,解得m=1或m=-5,
∴P点坐标为(1,0),(-5,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.

(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
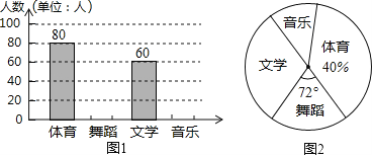
【题目】为了促进学生多样化发展,某中学每周五组织学生开展社团活动,分别设置了体育、舞蹈、文学、音乐社团(要求人人参加社团,并且每人只能参加一项),为了解学生喜欢哪种社团活动,学校组织学生会成员随机抽取部分学生进行问卷调查,根据收集到的数据,绘制成了两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(1)此次共调查了______名学生;
(2)将条形统计图补充完整;
(3)图2中音乐社团所在扇形的圆心角的度数为______;
(4)若该校共有学生1600人,估计该校喜爱体育社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备组织七年级160名学生参加社会实践活动,租用35座和45座两种客车共四辆,每种客车至少租1辆,可以坐不满.
(1)参加本次活动至少需几辆45座客车?
(2)如果35座客车的租金为每辆300元,45座客车的租金为每辆400元,要想使全部租车的费用不超过1550元,则有几种租车的方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD垂直于弦AC于点E,且交⊙O于点D,F是BA延长线上一点,若∠CDB=∠BFD.
(1)求证:FD是⊙O的一条切线;
(2)若AB=10,AC=8,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com