
【题目】已知二次函数y=a(x+m)2的顶点坐标为(﹣1,0),且过点A(﹣2,﹣![]() ).
).
(1)求这个二次函数的解析式;
(2)点B(2,﹣2)在这个函数图象上吗?
(3)你能通过左,右平移函数图象,使它过点B吗?若能,请写出平移方案.
【答案】(1)y=﹣![]() (x+1)2;(2)点B(2,﹣2)不在这个函数的图象上;(3)抛物线向左平移1个单位或平移5个单位函数,即可过点B;
(x+1)2;(2)点B(2,﹣2)不在这个函数的图象上;(3)抛物线向左平移1个单位或平移5个单位函数,即可过点B;
【解析】
(1)根据待定系数法即可得出二次函数的解析式;
(2)代入B(2,-2)即可判断;
(3)根据题意设平移后的解析式为y=-![]() (x+1+m)2,代入B的坐标,求得m的植即可.
(x+1+m)2,代入B的坐标,求得m的植即可.
(1)∵二次函数y=a(x+m)2的顶点坐标为(﹣1,0),
∴m=1,
∴二次函数y=a(x+1)2,
把点A(﹣2,﹣![]() )代入得a=﹣
)代入得a=﹣![]() ,
,
则抛物线的解析式为:y=﹣![]() (x+1)2.
(x+1)2.
(2)把x=2代入y=﹣![]() (x+1)2得y=﹣
(x+1)2得y=﹣![]() ≠﹣2,
≠﹣2,
所以,点B(2,﹣2)不在这个函数的图象上;
(3)根据题意设平移后的解析式为y=﹣![]() (x+1+m)2,
(x+1+m)2,
把B(2,﹣2)代入得﹣2=﹣![]() (2+1+m)2,
(2+1+m)2,
解得m=﹣1或﹣5,
所以抛物线向左平移1个单位或平移5个单位函数,即可过点B.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点(点
上的动点(点![]() 与点
与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,联结
,联结![]() ,点
,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 、
、![]() 作直线,交
作直线,交![]() 于点
于点![]() ,联结
,联结![]() 、
、![]() .
.
(1)当点![]() 在边
在边![]() 上,设
上,设![]() ,
,![]() .
.
①写出![]() 关于
关于![]() 的函数关系式及定义域;
的函数关系式及定义域;
②判断![]() 的形状,并给出证明;
的形状,并给出证明;
(2)如果![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象抛物线G经过(﹣5,0),(0,![]() ),(1,6)三点,直线l的解析式为y=2x﹣3
),(1,6)三点,直线l的解析式为y=2x﹣3
(1)求抛物线G的函数解析式;
(2)求证:抛物线G与直线L无公共点;
(3)若与l平行的直线y=2x+m与抛物线G只有一个公共点P,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
销售单价x(元/件) | … | 55 | 60 | 70 | 75 | … |
一周的销售量y(件) | … | 450 | 400 | 300 | 250 | … |
(1)直接写出y与x的函数关系式: .
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
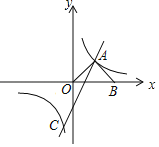
【题目】如图,在平面直角坐标系中,直线y1=2x﹣2与双曲线y2=![]() 交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
交于A、C两点,AB⊥OA交x轴于点B,且OA=AB.
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出y1<y2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节能又环保的油电混合动力汽车,既可以用油做动力行驶,也可以用电做动力行驶.比亚迪油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为![]() 元;若完全用电做动力行驶,则费用为
元;若完全用电做动力行驶,则费用为![]() 元,已知汽车行驶中每千米用油费用比用电费用多
元,已知汽车行驶中每千米用油费用比用电费用多![]() 元.
元.
(1)求:汽车行驶中每千米用电费用是多少元?甲乙两地的距离是多少千米?
(2)若汽车从甲地到乙地采用油电混合动力行驶,且所需费用不超过![]() 元,则至少需要用电行驶多少千米?
元,则至少需要用电行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个商场出售相同的某种商品,每件售价均为3000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一件按原售价收费,其余每件优惠30%;乙商场的优惠条件是:每件优惠25%.设所买商品为x件时,甲商场收费为y1元,乙商场收费为y2元.
(1)分别求出y1,y2与x之间的关系式;
(2)当甲、乙两个商场的收费相同时,所买商品为多少件?
(3)当所买商品为5件时,应选择哪个商场更优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点O是坐标原点,反比例函数y=![]() 的图像经过A(
的图像经过A(![]() ,1).
,1).
(1)求此反比例函数的解析式;
(2)将线段OA绕O逆时针旋转30°得到线段OB,判断点B是否在此反比例函数的图像上并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com