解:根据已知列表得:
| 圆的个数n | 1 | 2 | 3 | 4 | 5 | … | n |
| 平面区域数Sn | 2 | 4 | 7 | 11 | 16 | … | |
| 圆的交点数ak | 1 | 2 | 4 | 7 | 11 | … | |
则S
2-S
1=2,
S
3-S
2=3,
S
4-S
3=4,
S
5-S
4=5,
…
由此,不难推测:S
n-S
n-1=n.
把上面(n-1)个等式左、右两边分别相加,就得到:S
n-S
1=2+3+4+…+n,
∵S
1=2,
∴S
n=2+2+3+4+…+n=1+(1+2+3+4+…+n)=1+

=

.
∴n个圆过P点时,可把平面划分成

个平面区域;
同理:a
1=1,
a
2-a
1=1,
a
3-a
2=2,
a
4-a
3=3,
a
5-a
4=4,
…
a
n-1-a
n-2=n-2,
a
n-a
n-1=n-1.
n个式子相加a
n=1+(1+2+3+4+…+n-1)=1+
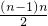
=
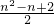
.
∴这n个圆共有
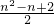
个交点.
分析:首先根据题意列表:
| 圆的个数n | 1 | 2 | 3 | 4 | 5 | … | n |
| 平面区域数Sn | 2 | 4 | 7 | 11 | 16 | … | |
| 圆的交点数ak | 1 | 2 | 4 | 7 | 11 | … | |
然后根据表格归纳规律,即可求得答案.
点评:本题考查了圆与圆的位置关系.属于规律型:图形的变化类题目.解题关键是由特殊到一般,其中第(1)题因为S
n-1为n-1个圆把平面划分的区域数,当再加上一个圆,即当n个圆过定点P时,这个加上去的圆必与前n-1个圆相交,所以这个圆就被前n-1个圆分成n部分,加在S
n-1上,所以有S
n=S
n-1+n.


 =
= .
. 个平面区域;
个平面区域;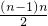 =
=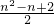 .
.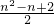 个交点.
个交点.
