
”¾ĢāÄæ”æ2019Äź5ŌĀ”°ŃĒÖŽĪÄĆ÷¶Ō»°“ó»į”±ŌŚ±±¾©³É¹¦¾Ł°ģ£¬ŅżĘšĮĖŹĄ½ēČĖĆńµÄ¼«“ó¹Ų×¢£¬Ä³ŹŠŅ»ŃŠ¾æ»ś¹¹ĪŖĮĖĮĖ½ā![]() ĖźÄźĮä¶ĪŹŠĆń¶Ō±¾“Ī“ó»įµÄ¹Ų×¢³Ģ¶Č£¬Ė껜єȔĮĖ100ĆūÄźĮäŌŚøĆ·¶Ī§ÄŚµÄŹŠĆń½ųŠŠĮĖµ÷²é£¬²¢½«ŹÕ¼Æµ½µÄŹż¾ŻÖĘ³ÉĮĖČēĻĀÉŠ²»ĶźÕūµÄʵŹż·Ö²¼±ķ”¢ĘµŹż·Ö²¼×ß·ĆĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£ŗ
ĖźÄźĮä¶ĪŹŠĆń¶Ō±¾“Ī“ó»įµÄ¹Ų×¢³Ģ¶Č£¬Ė껜єȔĮĖ100ĆūÄźĮäŌŚøĆ·¶Ī§ÄŚµÄŹŠĆń½ųŠŠĮĖµ÷²é£¬²¢½«ŹÕ¼Æµ½µÄŹż¾ŻÖĘ³ÉĮĖČēĻĀÉŠ²»ĶźÕūµÄʵŹż·Ö²¼±ķ”¢ĘµŹż·Ö²¼×ß·ĆĶ¼ŗĶÉČŠĪĶ³¼ĘĶ¼£ŗ
×鱚 | ÄźĮä¶Ī | ʵŹż£ØČĖŹż£© |
µŚ1×é |
| 5 |
µŚ2×é |
|
|
µŚ3×é |
| 35 |
µŚ4×é |
| 20 |
µŚ5×é |
| 15 |
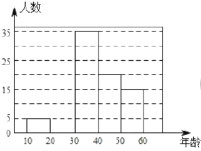
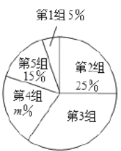
£Ø1£©ĒėÖ±½ÓŠ“³ö![]() ”¢
”¢![]() µÄÖµ¼°ÉČŠĪĶ³¼ĘĶ¼ÖŠµŚ3×éĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£»
µÄÖµ¼°ÉČŠĪĶ³¼ĘĶ¼ÖŠµŚ3×éĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø2£©Ēė²¹Č«ÉĻĆęµÄʵŹż·Ö²¼Ö±·½Ķ¼£»
£Ø3£©¼ŁÉčøĆŹŠĻÖÓŠ![]() ĖźµÄŹŠĆń300ĶņČĖ£¬ĪŹµŚ4×éÄźĮä¶Ī¹Ų×¢±¾“Ī“ó»įµÄČĖŹż¾ĻśÉĢÓŠ¶ąÉŁĶņČĖ£æ
ĖźµÄŹŠĆń300ĶņČĖ£¬ĪŹµŚ4×éÄźĮä¶Ī¹Ų×¢±¾“Ī“ó»įµÄČĖŹż¾ĻśÉĢÓŠ¶ąÉŁĶņČĖ£æ
”¾“š°ø”æ£Ø1£©20%£¬20£¬126”ć£»£Ø2£©¼ūĻź½ā£»£Ø3£©60ĶņČĖ
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāŗĶʵŹż·Ö²¼±ķÖŠµÄŹż¾Ż£¬æÉŅŌĒóµĆa”¢mµÄÖµŗĶµŚ3×éČĖŹżŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒµÄ¶ČŹż£»
£Ø2£©øł¾Ż£Ø1£©ÖŠaµÄÖµ£¬æÉŅŌ½«ĘµŹż·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£»
£Ø3£©øł¾ŻĘµŹż·Ö²¼±ķÖŠµÄŹż¾ŻæÉŅŌ¼ĘĖć³ö10”«60ĖźÄźĮä¶ĪµÄ¹Ų×¢±¾“Ī“ó»įµÄČĖŹżŌ¼ÓŠ¶ąÉŁ£®
½ā£ŗ£Ø1£©a£½100©5©35©20©15£½25£¬m%£½£Ø20”Ā100£©”Į100%£½20%£¬
”ąm£½20£¬
µŚ3×éČĖŹżŌŚÉČŠĪĶ³¼ĘĶ¼ÖŠĖł¶ŌÓ¦µÄŌ²ŠÄ½ĒŹĒ£ŗ![]() £¬
£¬
£Ø2£©ÓÉ£Ø1£©ÖŖ£¬20”Üx£¼30£¬ÓŠ25ČĖ£¬
²¹Č«µÄʵŹż·Ö²¼Ö±·½Ķ¼ČēĻĀ£ŗ
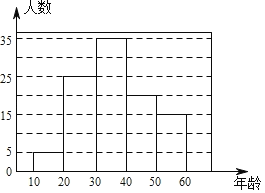
£Ø3£©![]() £ØĶņČĖ£©£¬
£ØĶņČĖ£©£¬
“š£ŗµŚ4×éÄźĮä¶ĪµÄ¹Ų×¢±¾“Ī“ó»įµÄČĖŹżŌ¼ÓŠ60ĶņČĖ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
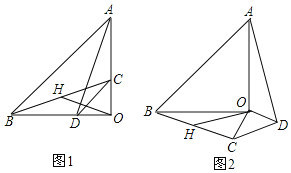
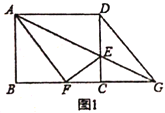
”¾ĢāÄæ”æŅŃÖŖ£ŗ”÷AOBŗĶ”÷COD¾łĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬”ĻAOB£½”ĻCOD£½90”ć£¬AO£½4£¬CO£½2£¬½ÓĮ¬½ÓAD£¬BC”¢µćHĪŖBCÖŠµć£¬Į¬½ÓOH£®
£Ø1£©ČēĶ¼1ĖłŹ¾£¬ĒóÖ¤£ŗOH£½![]() ADĒŅOH”ĶAD£»
ADĒŅOH”ĶAD£»
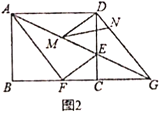
£Ø2£©½«”÷CODČʵćOŠż×Ŗµ½Ķ¼2ĖłŹ¾Ī»ÖĆŹ±£¬Ļ߶ĪOHÓėADÓÖÓŠŌõŃłµÄ¹ŲĻµ£¬Ö¤Ć÷ÄćµÄ½įĀŪ£»
£Ø3£©ĒėÖ±½ÓŠ“³öĻ߶ĪOHµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£Ø1£©£¬ŅŃÖŖŠ”Õż·½ŠĪABCDµÄĆ껿ĪŖ1£¬°ŃĖüµÄø÷±ßŃÓ³¤Ņ»±¶µĆµ½ŠĀÕż·½ŠĪA1B1C1D1£»°ŃÕż·½ŠĪA1B1C1D1±ß³¤°“Ō·ØŃÓ³¤Ņ»±¶µĆµ½Õż·½ŠĪA2B2C2D2£ØČēĶ¼£Ø2£©£©£»Õż·½ŠĪA2B2C2D2µÄĆ껿ĪŖ________£¬ŅŌ“ĖĻĀČ„”£¬ŌņÕż·½ŠĪAnBnCnDnµÄĆ껿ĪŖ________£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬½«
£¬½«![]() Čʵć
Čʵć![]() °“ÄꏱÕė·½ĻņŠż×Ŗ£¬µĆµ½
°“ÄꏱÕė·½ĻņŠż×Ŗ£¬µĆµ½![]() £®
£®
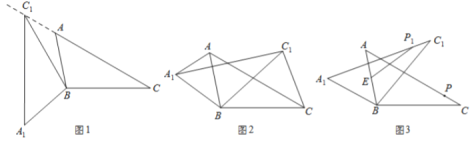
£Ø1£©ČēĶ¼ 1£¬µ±µć![]() ŌŚĻ߶Ī
ŌŚĻ߶Ī![]() µÄŃÓ³¤ĻßÉĻŹ±£¬Ēó
µÄŃÓ³¤ĻßÉĻŹ±£¬Ēó![]() µÄ¶ČŹż£»
µÄ¶ČŹż£»
£Ø2£©ČēĶ¼ 2£¬Į¬½Ó![]() £¬
£¬![]() £®Čō
£®Čō![]() µÄĆ껿ĪŖ 3£¬Ēó
µÄĆ껿ĪŖ 3£¬Ēó![]() µÄĆ껿£»
µÄĆ껿£»
£Ø3£©ČēĶ¼ 3£¬µć![]() ĪŖĻ߶Ī
ĪŖĻ߶Ī![]() ÖŠµć£¬µć
ÖŠµć£¬µć![]() ŹĒĻ߶Ī
ŹĒĻ߶Ī![]() ÉĻµÄ¶Æµć£¬ŌŚ
ÉĻµÄ¶Æµć£¬ŌŚ![]() Čʵć
Čʵć![]() °“ÄꏱÕė·½ĻņŠż×ŖµÄ¹ż³ĢÖŠ£¬µć
°“ÄꏱÕė·½ĻņŠż×ŖµÄ¹ż³ĢÖŠ£¬µć![]() µÄ¶ŌÓ¦µćŹĒµć
µÄ¶ŌÓ¦µćŹĒµć![]() £¬ĒóĻ߶Ī
£¬ĒóĻ߶Ī![]() ³¤¶ČµÄ×ī“óÖµÓė×īŠ”Öµ£®
³¤¶ČµÄ×ī“óÖµÓė×īŠ”Öµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½³µ·Ö±š“ÓĻą¾ą420kmµÄA”¢BĮ½µŲĻąĻņ¶ųŠŠ£¬ŅŅ³µ±Č¼×³µĻČ³ö·¢1Š”Ź±£¬Į½³µ·Ö±šŅŌø÷×ŌµÄĖŁ¶ČŌČĖŁŠŠŹ»£¬Ķ¾¾CµŲ£ØA”¢B”¢CČżµŲŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£©£®¼×³µµ½“ļCµŲŗóŅņÓŠŹĀĮ¢¼“°“ŌĀ·ŌĖŁ·µ»ŲAµŲ£¬ŅŅ³µ“ÓBµŲÖ±“ļAµŲ£¬¼×”¢ŅŅĮ½³µ¾ąø÷×Ō³ö·¢µŲµÄĀ·³Ģy£ØĒ§Ć×£©Óė¼×³µŠŠŹ»ĖłÓƵď±¼äx£ØŠ”Ź±£©µÄ¹ŲĻµČēĶ¼ĖłŹ¾£¬½įŗĻĶ¼ĻóŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©¼×³µµÄĖŁ¶ČŹĒ”” ””Ē§Ć×/Ź±£¬ŅŅ³µµÄĖŁ¶ČŹĒ”” ””Ē§Ć×/Ź±£»
£Ø2£©Ēó¼×³µ¾ąĖü³ö·¢µŲµÄĀ·³Ģy£ØĒ§Ć×£©ÓėĖüŠŠŹ»ĖłÓƵď±¼äx£ØŠ”Ź±£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©¼×³µ³ö·¢¶ą³¤Ź±¼äŗóĮ½³µĻą¾ą90Ē§Ć×£æĒėÄćÖ±½ÓŠ“³ö“š°ø£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£ŗŹżŃ§æĪÉĻ£¬ĄĻŹ¦³öŹ¾ĮĖÕāŃłŅ»øöĪŹĢā£ŗ
ČēĶ¼1£¬ŌŚµČ±ß![]() ÖŠ£¬µć
ÖŠ£¬µć![]() ”¢
”¢![]() ŌŚ
ŌŚ![]() ÉĻ£¬ĒŅ
ÉĻ£¬ĒŅ![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ½»
½»![]() ÓŚ
ÓŚ![]() µć£¬½»
µć£¬½»![]() ŃÓ³¤ĻßÓŚ
ŃÓ³¤ĻßÓŚ![]() µć£¬ĒŅ
µć£¬ĒŅ![]() £¬Ģ½¾æĻ߶Ī
£¬Ģ½¾æĻ߶Ī![]() Ö®¼äµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£®
Ö®¼äµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£®
Ä³Ń§Ļ°Š”×éµÄĶ¬Ń§¾¹żĖ¼æ¼£¬½»Į÷ĮĖ×Ō¼ŗµÄĻė·Ø£ŗ
Š”Ć÷£ŗ”°Ķعż¹Ū²ģŗĶ¶ČĮ棬·¢ĻÖ![]() Óė
Óė![]() “ęŌŚÄ³ÖÖŹżĮæ¹ŲĻµ”±£»
“ęŌŚÄ³ÖÖŹżĮæ¹ŲĻµ”±£»
Š”Ēæ£ŗ”°Ķعż¹Ū²ģŗĶ¶ČĮ棬·¢ĻÖĶ¼1ÖŠÓŠŅ»ĢõĻ߶ĪÓė![]() ĻąµČ”±£»
ĻąµČ”±£»
Š”Ī°£ŗ”°Ķعż¹¹ŌģČż½ĒŠĪ£¬Ö¤Ć÷Čż½ĒŠĪČ«µČ£¬½ų¶ųæÉŅŌµĆµ½Ļ߶Ī![]() Ö®¼äµÄŹżĮæ¹ŲĻµ”±£®
Ö®¼äµÄŹżĮæ¹ŲĻµ”±£®
””
ĄĻŹ¦£ŗ”°±£ĮōŌĢāĢõ¼ž£¬ŌŁ¹żµć![]() ×÷
×÷![]() ½»
½»![]() ÓŚ
ÓŚ![]() Óė
Óė![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() £ØČēĶ¼2£©Čē¹ūøų³ö
£ØČēĶ¼2£©Čē¹ūøų³ö![]() µÄÖµ£¬ÄĒĆ“æÉŅŌĒó³ö
µÄÖµ£¬ÄĒĆ“æÉŅŌĒó³ö![]() µÄÖµ”±£®
µÄÖµ”±£®
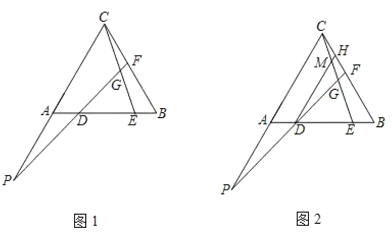
Ēė»Ų“š£ŗ
£Ø1£©ŌŚĶ¼1ÖŠÕŅ³ö![]() Óė
Óė![]() ŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£»
ŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£»
£Ø2£©ŌŚĶ¼1ÖŠÕŅ³öÓėĻ߶Ī![]() ĻąµČµÄĻ߶Ī£¬²¢Ö¤Ć÷£»
ĻąµČµÄĻ߶Ī£¬²¢Ö¤Ć÷£»
£Ø3£©Ģ½¾æĻ߶Ī![]() Ö®¼äµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£»
Ö®¼äµÄŹżĮæ¹ŲĻµ£¬²¢Ö¤Ć÷£»
£Ø4£©Čō![]() £¬Ēó
£¬Ēó![]() µÄÖµ£ØÓĆŗ¬
µÄÖµ£ØÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾£©£®
µÄ“śŹżŹ½±ķŹ¾£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
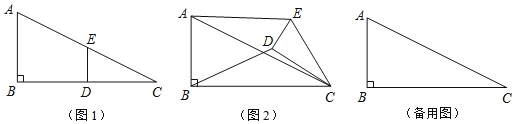
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ![]() ÖŠ£¬”ĻB=90”ć£¬
ÖŠ£¬”ĻB=90”ć£¬![]() £¬µćD£¬E·Ö±šŹĒ±ßBC£¬ACµÄÖŠµć£¬Į¬½Ó
£¬µćD£¬E·Ö±šŹĒ±ßBC£¬ACµÄÖŠµć£¬Į¬½Ó![]() ½«
½«![]() ČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ£¬¼ĒŠż×Ŗ½ĒĪŖ
ČʵćC°“Ė³Ź±Õė·½ĻņŠż×Ŗ£¬¼ĒŠż×Ŗ½ĒĪŖ![]() £®
£®
![]() ĪŹĢā·¢ĻÖ£ŗ
ĪŹĢā·¢ĻÖ£ŗ
![]() µ±
µ±![]() Ź±£¬
Ź±£¬![]() _____£»
_____£»![]() µ±
µ±![]() Ź±£¬
Ź±£¬![]() _____£®
_____£®
![]() ĶŲÕ¹Ģ½¾æ£ŗ
ĶŲÕ¹Ģ½¾æ£ŗ
ŹŌÅŠ¶Ļ£ŗµ±![]() Ź±£¬
Ź±£¬![]() µÄ“óŠ”ÓŠĪŽ±ä»Æ£æĒė½ö¾ĶĶ¼2µÄĒéæöøų³öÖ¤Ć÷£®
µÄ“óŠ”ÓŠĪŽ±ä»Æ£æĒė½ö¾ĶĶ¼2µÄĒéæöøų³öÖ¤Ć÷£®
![]() ĪŹĢā½ā¾ö£ŗ
ĪŹĢā½ā¾ö£ŗ
µ±![]() Šż×ŖÖĮA”¢D”¢EČżµć¹²Ļߏ±£¬Ö±½ÓŠ“³öĻ߶ĪBDµÄ³¤£®
Šż×ŖÖĮA”¢D”¢EČżµć¹²Ļߏ±£¬Ö±½ÓŠ“³öĻ߶ĪBDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ»ż¼«ĻģÓ¦”°ŗėŃļ“«Ķ³ĪĻƔ±µÄŗÅÕŁ£¬Ä³Ń§Š£³«µ¼Č«Š£1200Ćūѧɜ½ųŠŠ¾µäŹ«“ŹĖŠ±³»ī¶Æ£¬²¢ŌŚ»ī¶ÆÖ®ŗó¾Ł°ģ¾µäŹ«“Ź“óČü£¬ĪŖĮĖ½ā±¾“ĪĻµĮŠ»ī¶ÆµÄ³ÖŠųŠ§¹ū£¬Ń§Š£ĶÅĪÆŌŚ»ī¶ÆĘō¶ÆÖ®³õ£¬Ė껜³éČ”²æ·Öѧɜµ÷²é”°Ņ»ÖÜŹ«“ŹĖŠ±³ŹżĮæ”±£¬øłµ÷²é½į¹ū»ęÖĘ³ÉµÄĶ³¼ĘĶ¼£Ø²æ·Ö£©ČēĶ¼ĖłŹ¾£®
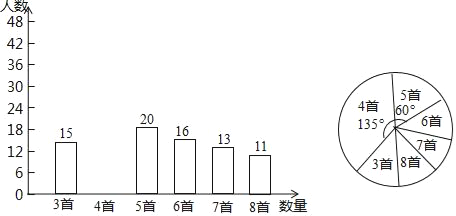
“óČü½įŹųŗóŅ»øöŌĀ£¬ŌŁ“Ī³é²éÕā²æ·Öѧɜ”°Ņ»ÖÜŹ«“ŹĖŠ±³ŹżĮæ”±£¬»ęÖĘ³ÉĶ³¼Ę±ķ
Ņ»ÖÜŹ«“ŹĖŠ±³ŹżĮæ | 3Ź× | 4Ź× | 5Ź× | 6Ź× | 7Ź× | 8Ź× |
ČĖŹż | 10 | 10 | 15 | 40 | 25 | 20 |
Ēėøł¾Żµ÷²éµÄŠÅĻ¢
£Ø1£©»ī¶ÆĘō¶ÆÖ®³õѧɜ”°Ņ»ÖÜŹ«“ŹĖŠ±³ŹżĮæ”±µÄÖŠĪ»ŹżĪŖ””””£»
£Ø2£©¹Ą¼Ę“óČüŗóŅ»øöŌĀøĆŠ£Ń§ÉśŅ»ÖÜŹ«“ŹĖŠ±³6Ź×£Øŗ¬6Ź×£©ŅŌÉĻµÄČĖŹż£»
£Ø3£©Ń”ŌńŹŹµ±µÄĶ³¼ĘĮ棬“ÓĮ½øö²»Ķ¬µÄ½Ē¶Č·ÖĪöĮ½“Īµ÷²éµÄĻą¹ŲŹż¾Ż£¬ĘĄ¼ŪøĆŠ£¾µäŹ«“ŹĖŠ±³ĻµĮŠ»ī¶ÆµÄŠ§¹ū£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬
£¬![]() ŹĒ
ŹĒ![]() ±ßÉĻŅ»µć£¬Į¬½Ó
±ßÉĻŅ»µć£¬Į¬½Ó![]() £¬½«¾ŲŠĪ
£¬½«¾ŲŠĪ![]() ŃŲ
ŃŲ![]() ÕŪµž£¬¶„µć
ÕŪµž£¬¶„µć![]() Ē”ŗĆĀäŌŚ
Ē”ŗĆĀäŌŚ![]() ±ßÉĻµć
±ßÉĻµć![]() “¦£¬ŃÓ³¤
“¦£¬ŃÓ³¤![]() ½»
½»![]() µÄŃÓ³¤ĻßÓŚµć
µÄŃÓ³¤ĻßÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £®
£®
£Ø1£©Ēó![]() µÄÖµ£»
掙术
£Ø2£©ĒóÖ¤£ŗĖıߊĪ![]() ŹĒĮāŠĪ£»
ŹĒĮāŠĪ£»
£Ø3£©ČēĶ¼2£¬![]() £¬
£¬![]() ·Ö±šŹĒĻ߶Ī
·Ö±šŹĒĻ߶Ī![]() £¬
£¬![]() ÉĻµÄ¶Æµć£ØÓė¶Ėµć²»ÖŲŗĻ£©£¬ĒŅ
ÉĻµÄ¶Æµć£ØÓė¶Ėµć²»ÖŲŗĻ£©£¬ĒŅ![]() £¬Éč
£¬Éč![]() £¬
£¬![]() £¬Ēė½ā¾öŅŌĻĀĻą¹ŲĪŹĢā£ŗ
£¬Ēė½ā¾öŅŌĻĀĻą¹ŲĪŹĢā£ŗ
¢ŁŠ“³ö![]() ¹ŲÓŚ
¹ŲÓŚ![]() µÄŗÆŹż½āĪöŹ½£»
µÄŗÆŹż½āĪöŹ½£»
¢ŚŹĒ·ń“ęŌŚÕāŃłµÄµć![]() £¬Ź¹
£¬Ź¹![]() ŹĒµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö
ŹĒµČŃüČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö![]() µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com