
分析 (1)首先去掉括号,再合并同类项,化简该代数式即可,注意去括号时符号的变化;
(2)首先把化简后的代数式因式分解,然后根据偶次方的非负性判断,判断出该说法不正确,再举出一个反例加以说明即可.
解答 解:(1)(x-2)2-2(x+3)(x-3)-23
=(x2-4x+4)-2(x2-9)-23
=x2-4x+4-2x2+18-23
=-x2-4x-1
(2)-x2-4x-1
=-(x2+4x+4)+3
=-(x+2)2+3
根据偶次方的非负性,可得-(x+2)2≤0,
但是-(x+2)2+3的值不一定是负数,
例如当x=-1时,
-(x+2)2+3
=-(-1+2)2+3
=-1+3
=2
所以有人认为不论x取何值该代数式的值均为负数,我认为不正确.
故答案为:不正确.
点评 (1)此题主要考查了因式分解方法的应用,以及整式的化简,要熟练掌握,解答此题的关键是注意去括号时符号的变化.
(2)此题还考查了偶次方的非负性,要熟练掌握,解答此题的关键是要明确:任意一个数的偶次方都是非负数.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点C可能是线段AB的中点 | |
| B. | 点D一定不是线段AB的中点 | |
| C. | 点C,D可能同时在线段AB上 | |
| D. | 点C,D可能同时在线段AB的延长线上 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
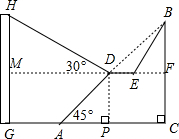 市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).
市政府对城市建设进行了整改,如图,已知斜坡AB长90$\sqrt{2}$米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(后两个小题结果都保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com