
如图1,在菱形ABCD中,AC=2,BD=![]() ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板600角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板600角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.

解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,
∴△AOB为直角三角形,且OA=![]() AC=1,OB=
AC=1,OB=![]() BD=
BD=![]() .
.
在Rt△AOB中,由勾股定理得:
AB=![]() =
=![]() =2.
=2.
(2)①△AEF是等边三角形.理由如下:
∵由(1)知,菱形边长为2,AC=2,
∴△ABC与△ACD均为等边三角形,
∴∠BAC=∠BAE+∠CAE=60°,
又∵∠EAF=∠CAF+∠CAE=60°,
∴∠BAE=∠CAF.
在△ABE与△ACF中,
∵ ,
,
∴△ABE≌△ACF(ASA),
∴AE=AF,
∴△AEF是等腰三角形,
又∵∠EAF=60°,
∴△AEF是等边三角形.
②BC=2,E为四等分点,且BE>CE,
∴CE=![]() ,BE=
,BE=![]() .
.
由①知△ABE≌△ACF,
∴CF=BE=![]() .
.
∵∠EAC+∠AEG+∠EGA=∠GFC+∠FCG+∠CGF=180°(三角形内角和定理),
∠AEG=∠FCG=60°(等边三角形内角),
∠EGA=∠CGF(对顶角)
∴∠EAC=∠GFC.
在△CAE与△CFG中,
∵![]() ,
,
∴△CAE∽△CFG,
∴![]() ,即
,即![]() ,
,
解得:CG=![]() .
.


科目:初中数学 来源: 题型:阅读理解
| PG |
| PC |
| PG |
| PC |
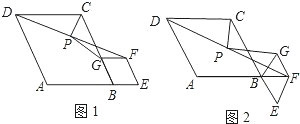 原问题中的其他条件不变,请你直接写出
原问题中的其他条件不变,请你直接写出| PG |
| PC |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 4 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com