某商场准备进一批不同型号的衣服,若购进A种型号衣服5件,B种型号衣服3件,则共需750元;若购进A种型号衣服2件,B种型号衣服5件,则共需680元;已知销售一件A型号衣服可获利12元,销售一件B型号衣服可获利20元,要使在这次销售中获利不少于510元,且A型号衣服的数量不多于28件.
(1)求A、B型号衣服进价各是多少元?
(2)若购进A型号衣服的数量是B型号衣服的2倍还多4件,则商店在这次进货中可有几种方案?并简述购货方案.
解:(1)设A型号的衣服进价每件x元,B型号衣服每件进价y元,由题意得:
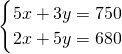
,
解得:
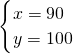
.
答:A型号的衣服进价每件90元,B型号衣服每件进价100元.
(2)设购买B型号的衣服m件,则购买A型号的衣服(2m+4),由题意,得
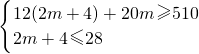
,
解得:10.5≤m≤12,
∵m为整数,
∴m=11,12,
当m=11时,购买A型号的衣服:2×11+4=26件,
当m=12时,购买A型号的衣服:2×12+4=28件.
∴进货方案有:①A型号衣服26件,B型号衣服11件;②A型号衣服28件,B型号衣服12件.
分析:(1)设A型号的衣服进价每件x元,B型号衣服每件进价y元,由题意可以得出5x+3y=750,2x+5y=680,由这两个方程建立方程组求出其解就可以了.
(2)设购买B型号的衣服m件,则购买A型号的衣服(2m+4),根据总利润=单件利润×数量建立不等式12(2m+4)+20m≥510,及2m+4≤28,构成不等式组求出其解就可以得出答案.
点评:本题考查了列二元一次方程组解实际问题的运用及列一元一次不等式组解实际问题的运用,在解答时建立方程和不等式是关键.

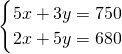 ,
,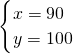 .
.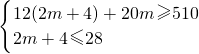 ,
,
