
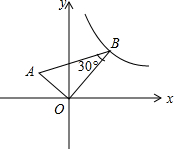
 如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点B在y=$\frac{3}{x}$的图象上,求过点A的反比例函数的解析式.
如图,在平面直角坐标系中,AO⊥BO,∠B=30°,点B在y=$\frac{3}{x}$的图象上,求过点A的反比例函数的解析式. 分析 作AD⊥x轴于D,BE⊥x轴于E,如图,设B(m,$\frac{3}{m}$),在Rt△ABO中利用含30度的直角三角形三边的关系得OB=$\sqrt{3}$OA,再证明Rt△AOD∽Rt△OBE,利用相似比得到AD=$\frac{\sqrt{3}}{3}$m,OD=$\frac{\sqrt{3}}{m}$,则A点坐标为(-$\frac{\sqrt{3}}{m}$,$\frac{\sqrt{3}}{3}$m),设点B所在反比例函数的解析式为y=$\frac{k}{x}$,然后根据反比例函数图象上点的坐标特征易得k=-$\frac{\sqrt{3}}{m}$•$\frac{\sqrt{3}}{3}$m=-1,从而得到反比例函数解析式.
解答 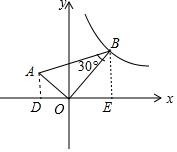 解:作AD⊥x轴于D,BE⊥x轴于E,如图,设B(m,$\frac{3}{m}$)
解:作AD⊥x轴于D,BE⊥x轴于E,如图,设B(m,$\frac{3}{m}$)
在Rt△ABO中,∵∠B=30°,
∴OB=$\sqrt{3}$OA,
∵∠AOD=∠OBE,
∴Rt△AOD∽Rt△OBE,
∴$\frac{AD}{OE}$=$\frac{OD}{BE}$$\frac{OA}{OB}$=,即$\frac{AD}{m}$=$\frac{OD}{\frac{3}{m}}$=$\frac{1}{\sqrt{3}}$,
∴AD=$\frac{\sqrt{3}}{3}$m,OD=$\frac{\sqrt{3}}{m}$,
∴A点坐标为(-$\frac{\sqrt{3}}{m}$,$\frac{\sqrt{3}}{3}$m),
设点A所在反比例函数的解析式为y=$\frac{k}{x}$,
∴k=-$\frac{\sqrt{3}}{m}$•$\frac{\sqrt{3}}{3}$m=-1,
∴点B所在反比例函数的解析式为y=-$\frac{1}{x}$.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了相似三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
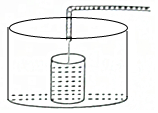 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )| A. |  | B. |  | C. |  | D. | 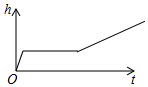 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
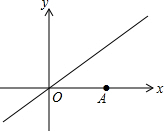 如图,点A坐标为(2,0),在直线y=$\frac{\sqrt{3}}{3}$x上取点M,使△AOM为等腰三角形,则满足条件的M坐标为(-$\sqrt{3}$,-1),($\sqrt{3}$,1),(3,$\sqrt{3}$),(1,$\frac{\sqrt{3}}{3}$).
如图,点A坐标为(2,0),在直线y=$\frac{\sqrt{3}}{3}$x上取点M,使△AOM为等腰三角形,则满足条件的M坐标为(-$\sqrt{3}$,-1),($\sqrt{3}$,1),(3,$\sqrt{3}$),(1,$\frac{\sqrt{3}}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
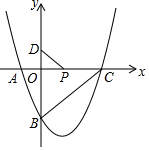 二次函数y=ax2-2x+c的图象与x轴交于A(-1,0),C(3,0),与y轴交于点B.
二次函数y=ax2-2x+c的图象与x轴交于A(-1,0),C(3,0),与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α(0°<α<180°),使点A仍在双曲线上,则α=30°.
如图,在反比例函数图象中,△AOB是等边三角形,点A在双曲线的一支上,将△AOB绕点O顺时针旋转α(0°<α<180°),使点A仍在双曲线上,则α=30°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com