
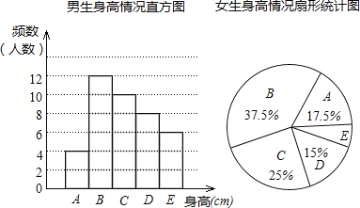
【题目】为了解某校七年级学生的身高情况,随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
组别 | 身高 |
A | 145≤x<155 |
B | 155≤x<160 |
C | 160≤x<165 |
D | 165≤x<170 |
E | 170≤x<175 |
根据图表提供的信息,回答下列问题:
(1)样本中,男生人数为 人,男生身高类别B的频率为 ;
(2)样本中,女生身高在E组的人数为 人,女生类别D的频数所对应的扇形圆心角为 ;
(3)已知该校共有男生400人,女生380人,请估计身高在160≤x<170之间的学生约有多少人?
【答案】(1)40,0.3;(2)2,54°;(3)332.
【解析】
(1)根据男生身高情况的频数分布直方图即可求得样本中的男生人数,用男生身高类别B的人数除以男生的总人数即可求得男生身高类别B的频率;(2)利用40乘以女生身高在E组人数所占的百分比即可求得女生身高在E组的人数,用360°乘以女生类别D的所占的百分比即可求得女生类别D的频数所对应扇形圆心角的度数;(3)用男生400人乘以男生身高在160≤x<170之间的频率即可求得男生身高在160≤x<170的人数,再利用女生380人乘以女生身高在160≤x<170之间所占的百分比即可求得女生身高在160≤x<170的人数,由此即可求解.
(1)男生人数为![]() 人,男生身高类别B的频率为:
人,男生身高类别B的频率为:![]() ;
;
故答案为:40,0.3;
(2)女生身高在E组的人数为:
![]() (人);
(人);
女生类别D的频数所对应扇形圆心角的度数为:
![]() ;
;
故答案为:2,54°;
(3)∵400×![]() +380×(25%+15%)=332(人),
+380×(25%+15%)=332(人),
∴估计身高在160x<170之间的学生约有332人.


科目:初中数学 来源: 题型:
【题目】把一张对边互相平行的纸条,折成如图所示,EF是折痕.若∠EFB=32°,则下列结论错误的有( ) 
A.∠C′EF=32°
B.∠AEC=148°
C.∠BGE=64°
D.∠BFD=116°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0, ![]() ).
).
(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1 , △BA′O的面积为S2 , S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△ABO的边AB垂直与x轴,垂足为点B,反比例函数y= ![]() (x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3,
(x>0)的图象经过AO的中点C,且与AB相交于点D,OB=4,AD=3, 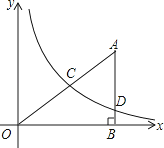
(1)求反比例函数y= ![]() 的解析式;
的解析式;
(2)求cos∠OAB的值;
(3)求经过C、D两点的一次函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y= ![]() 与直线y=﹣2x+2交于点A(﹣1,a).
与直线y=﹣2x+2交于点A(﹣1,a).
(1)求a,m的值;
(2)求该双曲线与直线y=﹣2x+2另一个交点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O,A,B,C的坐标分别为(0,0),(-1,2),(-3,3)和(-2,1).
(1)若图中的各个点的纵坐标不变,横坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.
(2)若图中的各个点的横坐标不变,纵坐标都乘-1,与原图案相比,所得图案有什么变化?画出图形并说明一下变化.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面图象表示小红从家里出发去散步过程中离家的距离s(米)与散步所用的时间t(分)之间的关系,请根据图象,确定下面描述符合小红散步情景的是( )
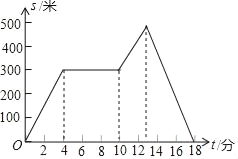
A. 从家出发,到了一个公共阅报栏,看了一会儿报,就回家了
B. 从家里出发,散了一会儿步,就找同学去了,18分钟后才开始返回
C. 从家里出发,一直散步(没有停留),然后回家了
D. 从家出发,到了一个公共阅报栏,看了一会儿报,继续向前走了一段后,然后回家了
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,
![]() 能确定59319的立方根是个两位数.
能确定59319的立方根是个两位数.
②![]() 59319的个位数是9,又
59319的个位数是9,又![]() ,
,
![]() 能确定59319的立方根的个位数是9.
能确定59319的立方根的个位数是9.
③如果划去59319后面的三位319得到数59,
而![]() ,则
,则![]() ,可得
,可得![]() ,
,
由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数110592,按这种方法求立方根,请完成下列填空.
①它的立方根是 位数.
②它的立方根的个位数是 .
③它的立方根的十位数是 .
④110592的立方根是 .
(2)请直接填写结果:
①![]() ;
;
②![]() ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com