
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,点
的中点,点![]() 为射线
为射线![]() 上一动点,连结
上一动点,连结![]() ,作
,作![]() 交射线
交射线![]() 于点
于点![]() .
.
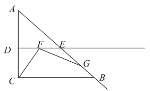
(1)当点![]() 在线段
在线段![]() 上时,求
上时,求![]() 与
与![]() 的大小关系;
的大小关系;
(2)当![]() 等于多少时,
等于多少时,![]() 是等腰三角形.
是等腰三角形.
【答案】(1)FG=FC(2) 6-3![]() 或3
或3![]() 或6+3
或6+3![]()
【解析】
(1)在DC上取一点M,使DM=DF,根据中位线和等腰直角三角形及线段的关系得到CM=EF,再判断出∠FCM=∠GFE,即可得出△EFG≌△MCF(ASA),即可求解;
(2)分点点F在DE上和DE的延长线上,构造直角三角形,建立方程求解即可得出结论.
(1)如图1,在DC上取一点M,使DM=DF,
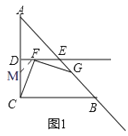
∵AC=BC,∠ACB=90![]() ,
,
∴∠A=∠ABC=45![]() ,
,
点D,E是AC,AB的中点,
∴DE=![]() BC=3,AD=CD=
BC=3,AD=CD=![]() AC=3,DE∥BC,
AC=3,DE∥BC,
∴CD=DE,∠ADE=∠CDE=∠ACB=90![]() ,∠AED=∠ABC=45
,∠AED=∠ABC=45![]()
∴CD-DM=DE-DF,
∴CM=EF,∠DMF=45![]() =∠AED,
=∠AED,
∴∠CMF=∠FEG,
∵CF⊥FG,
∴∠EFG+∠CFD=90![]() ,
,
∵∠DCF+∠CFD=90![]() ,
,
∴∠FCM=∠GFE,
在△EFG和△MCF中,

∴△EFG≌△MCF(ASA),
∴FG=FC;
(2)设DF=x,
∵AC=BC=6,
∴AB=![]()
∴BE=AE=![]() AB=3
AB=3![]()
①当点F在DE上时,如图2,

∵△BFG为等腰三角形,
∴FG=BG,
过点G作GN⊥DE于N,
∴∠FGN+∠GFN=90![]() ,
,
∵CF⊥FG
∴∠CFD+∠GFN=90![]() ,
,
∴∠CFD=∠FGN,
又CF=FG, ∠CDF=∠FNG=90![]()
∴△CDF≌△FNG,
∴FN=CD=3,
∴EN=DF=NG,
∴EG=![]() EN=
EN=![]() NG=
NG=![]() x,
x,
∴FG=BG=BE-EG=3![]() -
-![]() x,
x,
在Rt△FNG中,FG2NG2=FN2,
即:(3![]() -
-![]() x)2x2=9,
x)2x2=9,
∴x=6+3![]() (舍)或x=63
(舍)或x=63![]() ,
,
②当点F在DE的延长线上时,如图3

∵△BFG为等腰三角形,
Ⅰ、当BF=BG时,
过点B作BP⊥DE于P,
∴四边形BCDP是矩形,
∴BP=CD=3,DP=BC=6,
∴PF=DFDP=x6,
在图2中,FM=![]() DF=
DF=![]() x,
x,
∴EG=FM=![]() x,
x,
∴BF=BG=EGBE=![]() x3
x3![]() =
=![]() (x3),
(x3),
在Rt△BPF中,BF2PF2=BP2,
即:[![]() (x3)]2(x6)2=9.
(x3)]2(x6)2=9.
∴x=3![]() (舍)或x=3
(舍)或x=3![]() ,
,
Ⅱ、当BG=FG时,
BG=FG=CF=![]() ;EG=MF=
;EG=MF=![]() DF=
DF=![]() x;BE=3
x;BE=3![]()
∴![]() +3
+3![]() =
=![]() x,
x,
整理得:x212x+9=0
解得:x=6+3![]() 或x=63
或x=63![]() (不符题意舍去),
(不符题意舍去),
当BF=FG时,CF=FG=BF=![]() ,
,
∵CF=![]() ,
,
∴![]() =
=![]() ,
,
∴x=3(舍)
即:△BFG为等腰三角形时,x的值为6-3![]() 或3
或3![]() 或6+3
或6+3![]() .
.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】某校七年级10个班的300名学生即将参加学校举行的研究旅行活动,学校提出以下4个活动主题:A.赤水丹霞地貌考察;B.平塘天文知识考察;C.山关红色文化考察;D.海龙电土司文化考察,为了解学生喜欢的活动主题,学生会开展了一次调查研究,请将下面的过程补全
(1)收集数据:学生会计划调查学生喜欢的活动主题情况,下面抽样调查的对象选择合理的是______.(填序号)
①选择七年级3班、4班、5班学生作为调查对象
②选择学校旅游摄影社团的学生作为调查对象
③选择各班学号为6的倍数的学生作为调查对象
(2)整理、描述数据:通过调査后,学生会同学绘制了如下两幅不完整的统计图,请把统计图补充完整
某校七年级学生喜欢的活动主题条形统计图某校七年级学生喜欢的活动主题扇形统计图
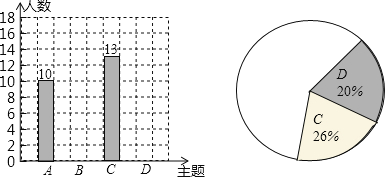
(3)分析数据、推断结论:请你根据上述调查结果向学校推荐本次活动的主题,你的推荐是______(填A-D的字母代号),估算全年级大约有多少名学生喜欢这个主题活动
(4)若在5名学生会干部(3男2女)中,随机选取2名同学担任活动的组长和副组长,求抽出的两名同学恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有两点![]() ,它们的对应数分别是
,它们的对应数分别是![]() ,其中
,其中![]()
![]()
(1)在![]() 左侧作线段
左侧作线段![]() ,在
,在![]() 的右侧作线段
的右侧作线段![]() (要求尺规作图,不写作法,保留作图痕迹)
(要求尺规作图,不写作法,保留作图痕迹)
(2)若点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是
对应的数是![]() ,且
,且![]() ,求
,求![]() 的值
的值
(3)在(2)的条件下,设点![]() 是
是![]() 的中点,
的中点,![]() 是数轴上一点,且
是数轴上一点,且![]() ,请直接写出
,请直接写出![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() ,以
,以![]() 为且在
为且在![]() 的右侧作正方形
的右侧作正方形![]() .
.

(1)如果![]() ,当点
,当点![]() 在线段BC上时(与点
在线段BC上时(与点![]() 不重合),①如图2,线段
不重合),①如图2,线段![]() 的数量关系为 ,线段
的数量关系为 ,线段![]() 所在直线的位置关系为 ;
所在直线的位置关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如,3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如,3,①中的结论是否仍然成立,并说明理由;
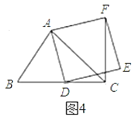
(2)如图4,如果![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),请直接写出答案.
不重合),请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植树4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.将各类的人数绘制成扇形图(如图1)和条形图(如图2),经确认扇形图是正确的,而条形图尚有一处错误.
回答下列问题:
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数和中位数;
(3)求这20名学生每人植树量的平均数,并估计这260名学生共植树多少棵?

查看答案和解析>>
科目:初中数学 来源: 题型:
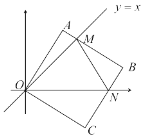
【题目】在平面直角坐标系中,边长为1的正方形![]() 的两个顶点
的两个顶点![]() ,
,![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 是原点.现在将正方形
是原点.现在将正方形![]() 绕原点
绕原点![]() 顺时针旋转,当点
顺时针旋转,当点![]() 第一次落在直线
第一次落在直线![]() 上时停止.旋转过程中,
上时停止.旋转过程中,![]() 边交直线
边交直线![]() 于点
于点![]() ,
,![]() 边交
边交![]() 轴于点
轴于点![]() .
.
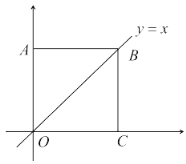
(1)若点![]() ,求此时点
,求此时点![]() 的坐标及
的坐标及![]() 的值;
的值;
(2)若![]() 的周长是
的周长是![]() ,在旋转过程中,
,在旋转过程中,![]() 值是否会发生变化?若不变,请求出这个定值,若有变化,请说明理由;
值是否会发生变化?若不变,请求出这个定值,若有变化,请说明理由;
(3)设![]() ,当
,当![]() 为何值时
为何值时![]() 的面积最小,最小值是多少?并直接写出此时
的面积最小,最小值是多少?并直接写出此时![]() 内切圆半径.
内切圆半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
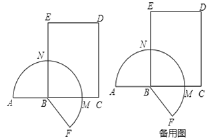
【题目】如图,点![]() 为长为5的线段
为长为5的线段![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() 于
于![]() ,且
,且![]() ,以
,以![]() 为邻边作矩形
为邻边作矩形![]() ,将线段
,将线段![]() 绕点B顺时针旋转,得到线段
绕点B顺时针旋转,得到线段![]() ,优弧
,优弧![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,设旋转角为
,设旋转角为![]()
(1)若扇形![]() 的面积为
的面积为![]() ,则
,则![]() 的度数为_______.
的度数为_______.
(2)连接![]() ,判断
,判断![]() 与扇形
与扇形![]() 所在圆
所在圆![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
(3)设![]() 为直线
为直线![]() 上一点,沿
上一点,沿![]() 所在直线折叠矩形,若折叠
所在直线折叠矩形,若折叠![]() 后所在的直线与扇形
后所在的直线与扇形![]() 所在
所在![]() 的相切,求
的相切,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com