
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题.
|


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
| A、a+(-b+c)=a-b-c |
| B、a+(b-c)=a+b-c |
| C、a-(b+c)=a+b-c |
| D、a-(b-c)=a-b-c |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直角坐标系中,过点A(0,2)的直线a垂直于y轴,M(9,2)为直线a上一点,若P点从M出发,以2cm/s的速度沿着直线a向左移动;点Q从原点同时出发,以1cm/s的速度沿x轴向右移动,当PQ∥y轴时,点P的运动时间为( )
如图,直角坐标系中,过点A(0,2)的直线a垂直于y轴,M(9,2)为直线a上一点,若P点从M出发,以2cm/s的速度沿着直线a向左移动;点Q从原点同时出发,以1cm/s的速度沿x轴向右移动,当PQ∥y轴时,点P的运动时间为( )| A、1s | B、2s | C、3s | D、4s |
查看答案和解析>>
科目:初中数学 来源: 题型:
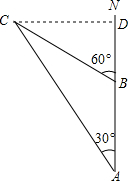 如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)?
如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com