试题分析:(1)因为ABCD为正方形,且边长为10,所以易得C点坐标;连接PM,根据P点坐标和半径求OM可得M点坐标;
(2)根据CM、PM、PC的长判定△PCM为直角三角形,得∠PMC=90°,从而判断相切;
(3)因CM长度固定,要使△QMC周长最小,只需PM+PC最小.作M关于x轴的对称点M′,连接CM′,交x轴于Q点,根据对称性及两点之间线段最短说明存在Q点.
(1)∵A(﹣2,0),B(8,0),
∴AB=10,
∵四边形ABCD为正方形,
∴BC=AB=10,
∴C(8,10),
连接MP,PC,
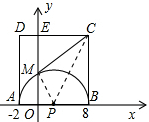
在Rt△OPM中,OP=3,MP=5,
∴OM=4,即M(0,4);
(2)在Rt△CBP中,CB=10,BP=5,
∴CP
2=125.
在Rt△CEM中,EM=6,CE=8,
∴CM
2=100,
∵100+25=125,
∴在△CMP中,CM
2+MP
2=CP
2,
∴∠CMP=90°.
即:PM⊥CM.
∴CM与⊙P相切.
(3)△QMC中,CM恒等于10,要使△QMC周长最小,即要使MQ+QC最小.故作M关于x轴对称点M’,连CM’交x轴于点Q,连MQ,此时,△QMC周长最小.
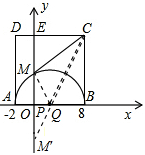
∵C(8,10),M'(0,﹣4),
设直线CM':y=kx+b(k≠0)
∴
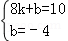
,解得
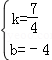
∴
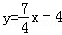
.
∴Q(
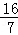
,0)
∵x轴垂直平分MM’,
∴QM=QM',
∴MQ+QC=M'Q+QC=M'C.
在△CEM'中,CE=8,EM'=14
∴
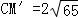
∴△QMC周长最小值为
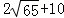
.
∴存在符合题意的点Q,且
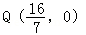
此时△QMC周长最小值为
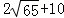
.
点评:解答本题的关键是熟记要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时熟练掌握两点之间线段最短在求三角形周长最短中的应用。

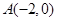 ,
, ,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.
,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.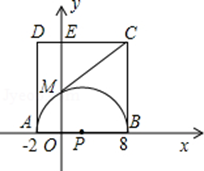
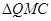 周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.
周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.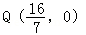 ,
,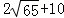

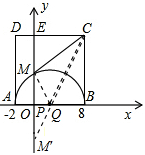
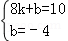 ,解得
,解得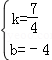
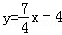 .
.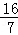 ,0)
,0)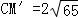
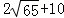 .
.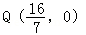
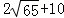 .
.

 ,求AD的长(结果保留根号).
,求AD的长(结果保留根号).