
| b |
| a |
| c |
| a |
 ¡ßx1£¼x2£¬
¡ßx1£¼x2£¬| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
| 1 |
| 2 |
| 27 |
| 4 |
| 27 |
| 2 |
| 1 |
| 2 |
| 27 |
| 2 |
| 1 |
| 2 |
| 27 |
| 2 |
| 27 |
| 4 |
| 27 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 4 |
| 13 |
| 13 |
| 27 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 4 |
| 27 |
| 4 |
| 13 |
| 27 |
| 4 |
| 13 |
| 27 |
| 4 |


 ÔĶÁ¿́³µÏµÁĐ´đ°¸
ÔĶÁ¿́³µÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£º½â´đ̀â
| 1 |
| 2 |
| 9 |
| 2 |
| 17 |
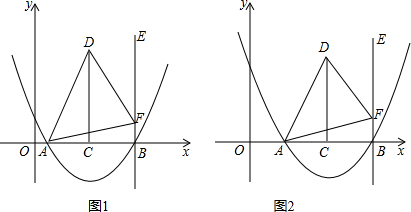
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£º½â´đ̀â
| PE |
| PF |
| PE |
| PF |
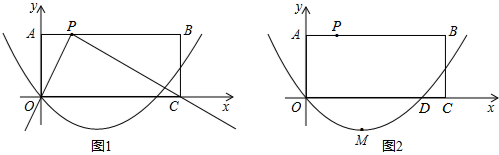
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£º½â´đ̀â
| 1 |
| 2 |
| 1 |
| 2 |

²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£º½â´đ̀â
| 1 |
| 50 |
| 49 |
| 50 |
| 194 |
| 5 |
| 13 |
| 55 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£º½â´đ̀â
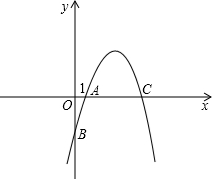
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£º½â´đ̀â

²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º²»Ïê ̀âĐÍ£ºµ¥Ñ¡̀â
| A£®y=x2-x-2 | B£®y=-
| ||||
C£®y=-
| D£®y=-x2+x+2 |

²é¿´´đ°¸ºÍ½âÎö>>
°Ù¶ÈÖÂĐÅ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com