
如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O 的切线交直线AC于点D,点E为CH的中点,连结并延交BD于点F,直线CF交AB的延长线于G.
⑴求证:AE·FD=AF·EC;
⑵求证:FC=FB;
⑶若FB=FE=2,求⊙O 的半径r的长.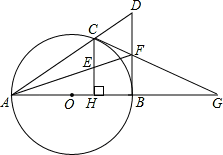
(1)证明:∵BD是⊙O的切线,∴∠DBA=90°。
∵CH⊥AB,∴CH∥BD。∴△AEC∽△AFD。
∴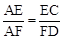 。∴AE•FD=AF•EC。
。∴AE•FD=AF•EC。
(2)证明:∵CH∥BD,∴△AEC∽△AFD,△AHE∽△ABF。∴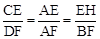 。
。
∵CE=EH(E为CH中点),∴BF=DF。
∵AB为⊙O的直径,∴∠ACB=∠DCB=90°。∴CF=DF=BF,即CF=BF。
(3)解:∵BF=CF=DF(已证),EF=BF=2,∴EF=FC。∴∠FCE=∠FEC。
∵∠AHE=∠CHG=90°,∴∠FAH+∠AEH=90°,∠G+∠GCH=90°。
∵∠AEH=∠CEF,∴∠G=∠FAG。∴AF=FG。
∵FB⊥AG,∴AB=BG。
连接OC,BC,
∵BF切⊙O于B,∴∠FBC=∠CAB。
∵OC=OA,CF=BF,
∴∠FCB=∠FBC,∠OCA=∠OAC
∴∠FCB=∠CAB。
∵∠ACB=90°,∴∠ACO+∠BCO=90°。∴∠FCB+∠BCO=90°,即OC⊥CG。
∴CG是⊙O切线。
∵GBA是⊙O割线,FB=FE=2,由切割线定理得:(2+FG)2=BG×AG=2BG2,
【注,没学切割线定理的可由△AGC∽△CGB求得】
在Rt△BFG中,由勾股定理得:BG2=FG2﹣BF2,∴FG2﹣4FG﹣12=0。
解得:FG=6,FG=﹣2(舍去)。
由勾股定理得:AB=BG= 。
。
∴⊙O的半径r是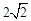 。
。
解析


科目:初中数学 来源: 题型:
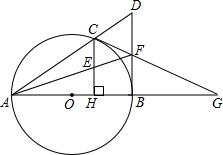 (2012•德阳)如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(2012•德阳)如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知点M是以AB为直径的半圆上的一个三等分点,点N是弧BM的中点,点P是直径AB上的点.若⊙O的半径为1.
如图,已知点M是以AB为直径的半圆上的一个三等分点,点N是弧BM的中点,点P是直径AB上的点.若⊙O的半径为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com