
| A | B | |
| 成本(万元/辆) | 6 | 12 |
| 售价(万元/辆) | 9 | 16 |
分析 (1)设购A种汽车x件,则B种汽车为80-x件,根据题意,可得,660≤6x+12(80-x)≤672,解出x的值,即可得到进货方案;
(2)根据题意,可得到,利润与购A种汽车的一次函数,即可解答哪种利润最大;
(3)根据题意,可得到,利润与购A种汽车的一次函数,根据a的取值,分类讨论解答;
解答 解:(1)设购A种汽车x件,则B种汽车为80-x件,根据题意得,
660≤6x+12(80-x)≤672,
解得48≤x≤50;有3种方案:
①购A种汽车48件、B种汽车为32件;
②购A种汽车49件、B种汽车为31件;
③购A种汽车50件、B种汽车为30件.
(2)由题意得,利润y=3x+4(80-x)=-x+320,
因为,函数y随x的增大而减小,
所以,当x=48时,即,当购A种汽车48件、B种汽车为32件时,
最大利润y=-1×48+320=272(万元);
(3)由题意得,利润y=(3+a)x+4(80-x)=(a-1)x+320,
∴当a>1时,购A种汽车50件、B种汽车为30件时,利润最大;
当a=1时,均可采用;
当0<a<1时,购A种汽车48件、B种汽车为32件时,利润最大.
点评 本题主要考查了一次函数在实际问题中的应用,弄清题意,先建立函数关系式,然后,根据实际情况,分类讨论解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
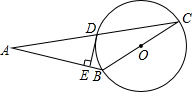 如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.
如图,在△ABC中,AB=BC,以BC为直径的⊙O与AC交于点D,DE⊥AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知 A(4,a),B(-2,-4)是一次函数y=kx+b的图象和反比例函y=$\frac{m}{x}$的图象的交点.
如图,已知 A(4,a),B(-2,-4)是一次函数y=kx+b的图象和反比例函y=$\frac{m}{x}$的图象的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com