
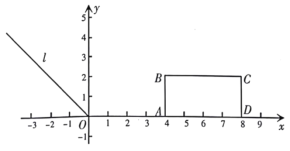
【题目】在平面直角坐标系中,已知长方形![]() ,点
,点![]() ,
,![]() .
.
(1)如图,有一动点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,若
上,若![]() ,求
,求![]() 的度数;
的度数;
(2)若把长方形![]() 向上平移,得到长方形
向上平移,得到长方形![]() .
.
①在运动过程中,求![]() 的面积与
的面积与![]() 的面积之间的数量关系;
的面积之间的数量关系;
②若![]() ,求
,求![]() 的面积与
的面积与![]() 的面积之比.
的面积之比.
【答案】(1)55°或35°;(2)①![]() ;②
;②![]() .
.
【解析】
(1)分两种情况:①在Rt△FEC中,求出∠FEC=90°-10°=80°,然后根据点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,得出∠POE=45°,对顶角相等,即可得出∠CPO=180°-80°-45°=55°;②由已知条件,得出∠CEO=45°,又根据∠CEO=∠CPE+∠PCB,得出∠CPO;
上,得出∠POE=45°,对顶角相等,即可得出∠CPO=180°-80°-45°=55°;②由已知条件,得出∠CEO=45°,又根据∠CEO=∠CPE+∠PCB,得出∠CPO;
(2)①首先设长方形![]() 向上平移
向上平移![]() 个单位长,得到长方形
个单位长,得到长方形![]() ,然后列出
,然后列出![]() 和
和![]() 的面积,即可得出两者的数量关系;
的面积,即可得出两者的数量关系;
②首先根据已知条件判定四边形![]() 是平行四边形,经过等量转化,即可得出
是平行四边形,经过等量转化,即可得出![]() 和
和![]() 的面积,进而得出其面积之比.
的面积,进而得出其面积之比.
(1)分两种情况:
①令PC交x轴于点E,延长CB至x轴,交于点F,如图所示:
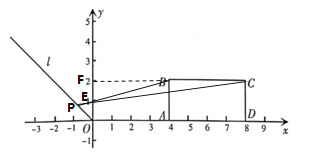
由已知得,![]() ,∠CFE=90°
,∠CFE=90°
∴∠FEC=90°-10°=80°,
又∵点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,
上,
∴∠POE=45°
又∵∠FEC=∠PEO=80°
∴∠CPO=180°-80°-45°=55°
②延长CB,交直线l于点E,
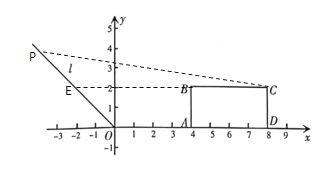
由已知得,![]() ,
,
∵点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,
上,
∴∠CEO=45°
∴∠CEO=∠CPE+∠PCB
∴∠CPO=45°-10°=35°.
故答案为55°或35°.
(2)如图,
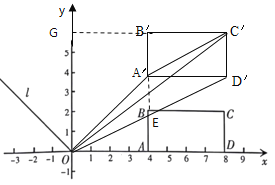
①设长方形![]() 向上平移
向上平移![]() 个单位长,得到长方形
个单位长,得到长方形![]()
![]()
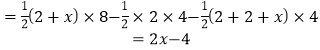
![]()
∴![]()
②∵长方形![]() ,
,
∴![]()
∵![]() ,
,
令![]() 交
交![]() 于E,
于E,
则四边形![]() 是平行四边形,
是平行四边形,
∴![]()
∴![]()
又∵![]()
由①得知,![]()
∴![]()
![]()
∴![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料,并用相关的思想方法解决问题.
计算:(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() ).
).
令![]() +
+![]() +
+![]() =t,则原式=(1﹣t)(t+
=t,则原式=(1﹣t)(t+![]() )﹣(1﹣t﹣
)﹣(1﹣t﹣![]() )t=t+
)t=t+![]() ﹣t2﹣
﹣t2﹣![]() t﹣
t﹣![]() t+t2=
t+t2=![]() ,
,
问题:
(1)计算:(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() )﹣(1﹣
)﹣(1﹣![]() ﹣
﹣![]() ﹣
﹣![]() )×(
)×(![]() +
+![]() +
+![]() );
);
(2)解方程(x2+5x+1)(x2+5x+7)=7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,长方形ABCD的边AB在y轴正半轴上,顶点A的坐标为(0,2),设顶点C的坐标为(a,b).
(1)顶点B的坐标为 ,顶点D的坐标为 (用a或b表示);
(2)如果将一个点的横坐标作为x的值,纵坐标作为y的值,代入方程2x+3y=12成立,就说这个点的坐标是方程2x+3y=12的解.已知顶点B和D的坐标都是方程2x+3y=12的解,求a,b的值;
(3)在(2)的条件下,平移长方形ABCD,使点B移动到点D,得到新的长方形EDFG,
①这次平移可以看成是先将长方形ABCD向右平移 个单位长度,再向下平移 个单位长度的两次平移;
②若点P(m,n)是对角线BD上的一点,且点P的坐标是方程2x+3y=12的解,试说明平移后点P的对应点P′的坐标也是方程2x+3y=12的解.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0, d)、C(-3,2).
(1)求d的值;
(2)将△ABC沿![]() 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
(3)在(2)的条件下,直线![]() 交y轴于点G,作
交y轴于点G,作![]() ⊥
⊥![]() 轴于
轴于![]() .
. ![]() 是线段
是线段![]() 上的一点,若△
上的一点,若△![]() 和△
和△![]() 面积相等,求点
面积相等,求点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在13×7的网格中,每个小正方形边长都是1,其顶点叫做格点,如图A、B、D、E、M、P均为格点.
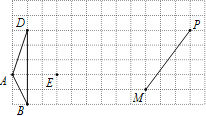
(1)请在网格中画□ABCD,要求C点在格点上.
(2)在(1)中□ABCD右侧画格点△EFG,并使EF=5,FG=3,EG=![]() .
.
(3)以MP为对角线画矩形MNPQ(M、N、P、Q按逆时针方向排列),使矩形MNPQ的面积为10.
(4)在直线AE上有一点W,使WB+WM的值最小,则这个最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
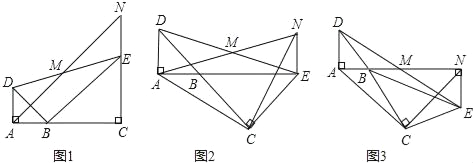
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),直接写出线段AD与NE的数量关系为 .
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),判断△ACN是什么特殊三角形并说明理由.
(3)将图1中△BCE绕点B旋转到图3位置,此时A,B,M三点在同一直线上.若AC=3![]() ,AD=1,则四边形ACEN的面积为 .
,AD=1,则四边形ACEN的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
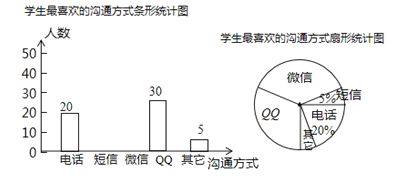
(1)这次统计共抽查了________名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为___________;
(2)请将条形统计图补充完整;
(3)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com