
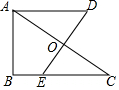
 如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$.
如图,Rt△ABC,∠B=90°,AC的垂直平分线交BC于点E,垂足为点O,过点A作BC的平行线,与直线OE交于点D,若AB=4,BC=6,则AD的长为$\frac{13}{3}$. 分析 直接利用勾股定理得出AC的长,再利用相似三角形的判定与性质得出EC的长,再利用全等三角形的判定与性质得出答案.
解答  解:如图所示:∵Rt△ABC,∠B=90°,AB=4,BC=6,
解:如图所示:∵Rt△ABC,∠B=90°,AB=4,BC=6,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{13}$,
∵AC的垂直平分线交BC于点E,
∴∠EOC=90°,AO=CO=$\sqrt{13}$,
又∵∠C=∠C,
∴△ACB∽△ECO,
∴$\frac{CO}{BC}$=$\frac{EC}{AC}$,
则$\frac{\sqrt{13}}{6}$=$\frac{EC}{2\sqrt{13}}$,
解得:EC=$\frac{13}{3}$,
∵AD∥BC,
∴∠DAC=∠C,
在△AOD和△COE中
∵$\left\{\begin{array}{l}{∠DAO=∠C}\\{AO=CO}\\{∠AOD=∠COE}\end{array}\right.$,
∴△AOD≌△COE(ASA),
∴EC=AD=$\frac{13}{3}$.
故答案为:$\frac{13}{3}$.
点评 此题主要考查了勾股定理以及相似三角形的判定与性质和全等三角形的判定与性质等知识,正确得出EC的长是解题关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
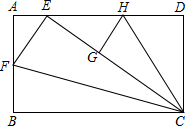 如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.
如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
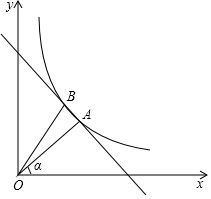 如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.
如图,在坐标系中,线段OA在第一象限,OA=5,OA与x轴的夹角α的正切tanα=$\frac{3}{4}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)图象经过点A,OA绕点O旋转后落在反比例函数y=$\frac{k}{x}$(x>0)的图象上另一点B,点B与x轴距离是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,B,C都在格点上,请按要求回答问题或画图:
如图,点A,B,C都在格点上,请按要求回答问题或画图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
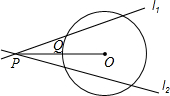 如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )
如图,点P为⊙O外一点,连结OP交⊙O于点Q,且PQ=OQ,经过点P的直线l1,l2,都与⊙O相交,则l1与l2所成的锐角α的取值范围是( )| A. | 0°<α<30° | B. | 0°<α<45° | C. | 0°<α<60° | D. | 0°<α<90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com