
 ��ƽ��ֱ������ϵ�У����ǰѹ���ԭ��ԳƵ����������߽����������á������ߣ�
��ƽ��ֱ������ϵ�У����ǰѹ���ԭ��ԳƵ����������߽����������á������ߣ����� ��1���Ƚ�������д�ɶ���ʽ���ٸ��ݡ������á������ߵĶ��弴�ɵĺ���������ʽ��
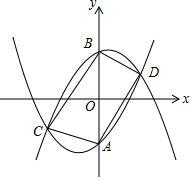
��2����ȷ����������y=x2+mx-4�ġ������á������ߵĽ���ʽ�������ó���A��B��C��D���꣬���ɵó�CD��AB��
���þ��ε����ʽ������̼������m��ֵ��
�ڸ����ı��ε������ʽ���ɽ���������⼴�ɵó����ۣ�
��� �⣺��1����������y=x2+3x-4=��x+$\frac{3}{2}$��2-$\frac{25}{4}$��
�ඥ������Ϊ��-$\frac{3}{2}$��-$\frac{25}{4}$����
���ݡ������á������ߵĶ���֪��������y=x2+3x-4�ġ������á������ߵĽ���ʽΪy=-��x-$\frac{3}{2}$��2+$\frac{25}{4}$=-x2+3x+4��
�ʴ�Ϊ����-$\frac{3}{2}$��-$\frac{25}{4}$����y=-x2+3x+4��
��2����������y=x2+mx-4=��x-$\frac{m}{2}$��2-$\frac{{m}^{2}+16}{4}$�٣�
��������ߵġ������á������߽���ʽΪy=-��x+$\frac{m}{2}$��2+$\frac{{m}^{2}+16}{4}$�ڣ�
��B��0��$\frac{{m}^{2}+16}{4}$����A��0��-$\frac{{m}^{2}+16}{4}$����
�����٢ڵã�C��-2��-2m����D��2��2m����
��AB=$\frac{{m}^{2}+16}{2}$��CD=$\sqrt{16+16{m}^{2}}$��
�١��ı���ACBDΪ���Σ�
��AB=CD��
��$\frac{{m}^{2}+16}{2}$=$\sqrt{16+16{m}^{2}}$��
��m=��2$\sqrt{2}$��
��m��0��
��m=2$\sqrt{2}$��
�ڵ�m��ֵ�����ı�ʱ���ı���ACBD������ǻᷢ���仯��
���ɣ����ݡ������á������ߵĶ��壬�ó��ı���ACBD��ƽ���ı��Σ�
��S�ı���ACBD=2S��ABD=AB��|xD|=$\frac{{m}^{2}+16}{2}$��2=m2+16��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�������¶��壬�������깫ʽ�����ε����ʣ�ƽ���ı��ε����ʣ��ı��ε������ʽ���Ȿ��Ĺؼ��������¶��壬�����¶��������⣮


 �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com