
【题目】解下列方程
(1)(x﹣1)2=4
(2)x2=3x
(3)2x2﹣x﹣1=0.
【答案】
(1)解:(x﹣1)2=4,
x﹣1=±2,
x﹣1=2,x﹣1=﹣2,
x1=3,x2=﹣1;
(2)解:x2=3x,
x2﹣3x=0,
x( x﹣3)=0,
x=0,x﹣3=0,
x1=0,x2=3;
(3)解:2x2﹣x﹣1=0,
(x﹣1)(2x+1)=0,
x1=1,x2=﹣ ![]() .
.
【解析】(1)两边开方,即可得出两个一元一次方程,求出方程的解即可.(2)移项后分解因式得出x(x﹣3)=0,推出x=0,x﹣3=0,求出方程的解即可.(3)等式的左边利用“十字相乘法”进行因式分解即可.
【考点精析】掌握因式分解法是解答本题的根本,需要知道已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势.


科目:初中数学 来源: 题型:
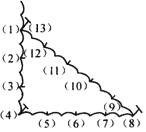
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,点D在半径OB的延长线上,∠BCD=∠A=30°. 
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径长为1,求由弧BC、线段CD和BD所围成的阴影部分面积.(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
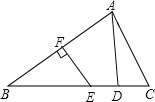
(1)求证:AD⊥BC.
(2)若∠BAC=75°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,AC=BC=10,AB=12.
(1)动手操作:利用尺规作以BC为直径的⊙O,⊙O交AB于点D,⊙O交AC于点E,并且过点D作DF⊥AC交AC于点F.
(2)求证:直线DF是⊙O的切线;
(3)连接DE,记△ADE的面积为S1 , 四边形DECB的面积为S2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )
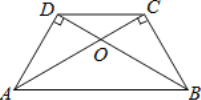
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s),则点Q的运动速度为 cm/s,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com