
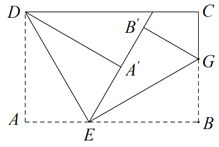
【题目】如图,将长方形纸片的一角作折叠,使顶点 A 落在 A处, DE 为折痕,将 BEA对折,使得 B落在直线 EA上,得折痕 EG .
(1)求 DEG 的度数;
(2) 若 EA恰好平分 DEB ,求 DEA的度数 .
科目:初中数学 来源: 题型:
【题目】“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.将这次调查情况整理并绘制如下两幅统计图如图2:

根据图中的信息,解答下列问题:
(1)本次活动共有 位市民参与调查;
(2)补全条形统计图和扇形统计图;
(3)扇形统计图中A项所对应的圆心角的度数为
(4)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”![]() 的各个数位上的数字之和记为
的各个数位上的数字之和记为![]() . 例如
. 例如![]() 时,
时,![]() .
.
(1)对于“相异数”![]() ,若
,若![]() ,请你写出一个
,请你写出一个![]() 的值;
的值;
(2)若![]() 都是“相异数”,其中
都是“相异数”,其中![]() ,
,![]() (
(![]() ,
,![]() 都是正整数),规定:
都是正整数),规定:![]() ,当
,当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形![]() ,对角线
,对角线![]() 交于点
交于点![]() ,点
,点![]() 分别是
分别是![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]()
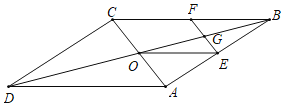
(1)证明:四边形![]() 是平行四边形
是平行四边形
(2)点![]() 是哪些线段的中点,写出结论,并选择一组给出证明.
是哪些线段的中点,写出结论,并选择一组给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个动点P在平面直角坐标系中按箭头所示方向作折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),……,按这样的运动规律,经过第2019次运动后,动点P的坐标是___________
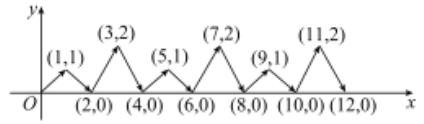
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
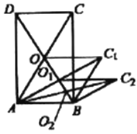
【题目】如图,矩形![]() 的面积为20,对角线
的面积为20,对角线![]() ,
,![]() 交于点
交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ,对角线交于点
,对角线交于点![]() ;以
;以![]() ,
,![]() 为邻边做平行四边形
为邻边做平行四边形![]() ;…;依此类推,则平行四边形
;…;依此类推,则平行四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.45
D.45
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com