
| 特产名称 | 三七 | 普洱茶 | 鲜花饼 |
| 每辆汽车运载量(吨) | 8 | 6 | 5 |
| 每吨特产利润(万元) | 1.2 | 1.6 | 1 |
分析 (1)根据题意可以得到运送鲜花饼的有(2x-1)辆,运送普洱茶的有[20-x-(2x-1)]辆,从而可以得到y与x的函数关系式;
(2)根据装运普洱茶的汽车不超过6辆,可以求得x的取值范围,从而可以得到y的最大值,从而可以得到总利润最大时,装运各种特产的车辆数.
解答 解:(1)由题意可得,
y=8x×1.2+5×(2x-1)×1+6×[20-x-(2x-1)]×1.6=-9.2x+196.6,
即y与x的函数关系式为y=-9.2x+196.6;
(2)由题意可得,
20-x-(2x-1)≤6,
解得,x≥5,
∵y=-9.2x+196.6,
∴当x=5时,y取得最大值,此时y=-9.2×5+196.6=150.6,2x-1=9,20-x-(2x-1)=20-5-9=6,
答:当总利润最大时,装运三七的有5辆车,装运普洱茶的有6辆车,装运鲜花饼的有9辆车,总利润最大值是150.6万元.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,求出相应的函数解析式,利用一次函数的性质求函数的最值.


科目:初中数学 来源: 题型:选择题
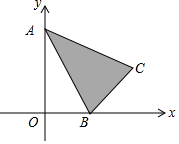 如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )
如图,已知△ABC的顶点坐标分别为A(0,2)、B(1,0)、C(2,1),若二次函数y=x2+bx+1的图象与阴影部分(含边界)一定有公共点,则实数b的取值范围是( )| A. | b≤-2 | B. | b<-2 | C. | b≥-2 | D. | b>-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
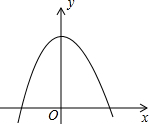 如图,若抛物线y=-x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=$\frac{k}{x}$(x>0)的图象是( )
如图,若抛物线y=-x2+3与x轴围成封闭区域(边界除外)内整点(点的横、纵坐标都是整数)的个数为k,则反比例函数y=$\frac{k}{x}$(x>0)的图象是( )| A. | 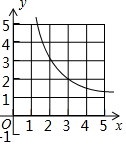 | B. | 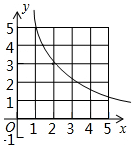 | C. | 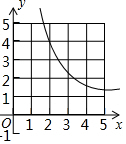 | D. | 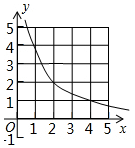 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
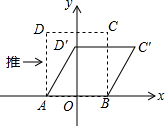 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )| A. | ($\sqrt{3}$,1) | B. | (2,1) | C. | (1,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y2<y3<y1 | D. | y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
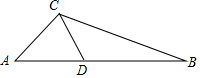 经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为113°或92°.
经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为113°或92°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com