
 如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB,AC上,AD交EF于交点H.
如图,在△ABC中,∠B=45°,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB,AC上,AD交EF于交点H.分析 (1)由已知条件易证△AHF∽△ADC,由相似三角形,列出比例关系式,即可证明;
(2)首先求出矩形EFPQ面积的表达式,然后利用二次函数求其最大面积.
解答 解:
(1)证明:∵四边形EFPQ是矩形,AH是△AEF的高,
∴EF∥BC,
∴△AHF∽△ADC,
∴AH:AD=AF:AC,
∵EF∥BC,
∴△AEF∽△ABC,
∴EF:BC=AF:AC,
∴$\frac{AH}{AD}=\frac{EF}{BC}$;
(2)解:∵∠B=45°,
∴BD=AD=4,
∴CD=BC-BD=5-4=1.
∵EF∥BC,
∴△AEH∽△ABD,
∴AH:AD=EH:BD,
∵EF∥BC,
∴△AFH∽△ACD,
∴AH:AD=HF:CD,
∴EH:BD=HF:CD,
即EH:4=HF:1,
∴EH=4HF,
已知EF=x,则EH=$\frac{4}{5}$x.
∵∠B=45°,
∴EQ=BQ=BD-QD=BD-EH=4-$\frac{4}{5}$x.
S矩形EFPQ=EF•EQ=x•(4-$\frac{4}{5}$x)=-$\frac{4}{5}$x2+4x=-$\frac{4}{5}$(x-$\frac{5}{2}$)2+5,
∴当x=$\frac{5}{2}$时,矩形EFPQ的面积最大,最大面积为5.
点评 本题是考查了相似三角形的判定与性质、二次函数的表达式与最值、矩形、等腰直角三角形等多个知识点,涉及考点较多,有一定的难度.


科目:初中数学 来源: 题型:解答题
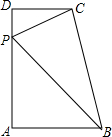 如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7;在AD上能找均一点P,使三角形PAB和三角形PCD相似?若能,共有几个符合条件的点P?并求相应PD的长,若不能,说明理由.
如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=2,AB=3,AD=7;在AD上能找均一点P,使三角形PAB和三角形PCD相似?若能,共有几个符合条件的点P?并求相应PD的长,若不能,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
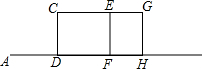 如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.
如图,A、B在一直线上,小明从点A出发沿AB方向匀速前进,4秒后走到点D,此时他(CD)在某一灯光下的影长为AD,继续沿AB方向以同样的速度匀速前进4秒后到点F,此时他(EF)的影长为2米,然后他再沿AB方向以同样的速度匀速前进2秒后达点H,此时他(GH)处于灯光正下方.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
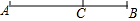 如图,点C在线段AB上,$\frac{AC}{AB}$=$\frac{CB}{AC}$,AB=1,AC=x,则x满足方程(整理成一般形式):x2+x-1=0,解之可求得线段AC=$\frac{-1+\sqrt{5}}{2}$,∴$\frac{AC}{AB}$=$\frac{-1+\sqrt{5}}{2}$=0.618.(精确到0.001)
如图,点C在线段AB上,$\frac{AC}{AB}$=$\frac{CB}{AC}$,AB=1,AC=x,则x满足方程(整理成一般形式):x2+x-1=0,解之可求得线段AC=$\frac{-1+\sqrt{5}}{2}$,∴$\frac{AC}{AB}$=$\frac{-1+\sqrt{5}}{2}$=0.618.(精确到0.001)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … | … | … | … |
| A. | 第251行,第1列 | B. | 第251行,第2列 | C. | 第252行,第1列 | D. | 第252行,第2列 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是(2n-1,2n-1).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则Bn的坐标是(2n-1,2n-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com