
 如图,已知等边△ABC,AE=BD,CE,AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:BG+DF=CE.
如图,已知等边△ABC,AE=BD,CE,AD交于点F,过点B作BG∥CE,BG交AD的延长线于点G,求证:BG+DF=CE. 分析 先证△ABD≌△CAE得CE=AD、∠AEC=∠ADB,进而有∠BDG=∠AEH,再证△GBD≌△HAE得BG=AH、∠H=∠G,由BG∥CE知∠G=∠CFG=∠AFH=∠H,从而得出AH=AF=BG,即可得证.
解答 证明:如图,作∠HAE=∠GBD,交CE延长线与点H,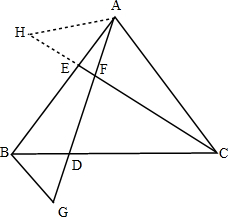
∵△ABC是等边三角形,
∴AB=AC,∠ABD=∠CAE=60°,
在△ABD和△CAE中,
∵$\left\{\begin{array}{l}{AB=CA}\\{∠ABD=∠CAE}\\{BD=AE}\end{array}\right.$,
∴△ABD≌△CAE(SAS),
∴CE=AD,∠AEC=∠ADB,
∵∠BDG=180°-∠ADB,∠AEH=180°-∠AEC,
∴∠BDG=∠AEH,
在△GBD和△HAE中,
∵∴$\left\{\begin{array}{l}{∠GBD=∠HAE}\\{BD=AE}\\{∠BDG=∠AEH}\end{array}\right.$,
∴△GBD≌△HAE(ASA),
∴BG=AH,∠H=∠G,
∵BG∥CE,
∴∠G=∠CFG=∠AFH=∠H,
∴AH=AF=BG,
故CE=AD=AF+DF=BG+DF,
即CE=BG+DF.
点评 本题主要考查全等三角形的判定和性质,添加辅助线将待证的线段用全等三角形联系到一起是关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 10x-6=12x+6 | B. | $\frac{x-6}{10}$=$\frac{x+6}{12}$ | C. | 10x+6=12x-6 | D. | $\frac{x+6}{10}$=$\frac{x-6}{12}$ |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省句容市华阳片七年级下学期第一次月考数学试卷(解析版) 题型:单选题
某花园内有一块五边形的空地如图所示,为了美化环境,现计划在五边形各顶点为圆心,2m长为半径的扇形区域(阴影部分)种上花草,那么种上花草的扇形区域总面积是( )

A. 6πm2 B. 5πm2 C. 4πm2 D. 3πm2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转一定角度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F.求证:
如图,在△ABC中,AB=BC,将△ABC绕点B顺时针旋转一定角度,得到△A1BC1,A1B交AC于点E,A1C1分别交AC,BC于点D,F.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
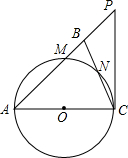 如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB,BC于点M,N,过点C作⊙O的切线交AB的延长线于点P.
如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB,BC于点M,N,过点C作⊙O的切线交AB的延长线于点P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com