
【题目】如图,在正方形ABCD中,E是AD上一点,F是BA延长线上的一点,AF=AE,.
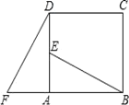
(1)求证:△ABE≌△ADF
(2)线段BE与DF有什么关系?证明你的结论.
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC>AB,E是AD上一点,△ABE沿BE折叠,点A恰好落在线段CE上的点F处.
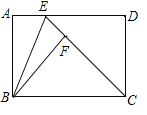
(1)求证:CF=DE;
(2)设![]() =m.
=m.
①若m=![]() ,试求∠ABE的度数;
,试求∠ABE的度数;
②设![]() =k,试求m与k满足的关系式.
=k,试求m与k满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注.某中学为了解该校九年级学生对观看“中国诗词大会”节目的喜爱程度,对该校九年级部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为:A 级(非常喜欢),B 级(较喜欢),C 级(一般),D 级(不喜欢).请结合两幅统计图,回答下列问题:

(1)本次抽样调查的样本容量是 ,表示“D级(不喜欢)”的扇形的圆心角为 °;
(2)若该校九年级有200名学生.请你估计该年级观看“中国诗词大会”节目B 级(较喜欢)的学生人数;
(3)若从本次调查中的A级(非常喜欢)的5名学生中,选出2名去参加广州市中学生诗词大会比赛,已知A级学生中男生有3名,请用“列表”或“画树状图”的方法求出所选出的2名学生中至少有1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,在△ABC中,AC=BC,∠ACB=90°,⊙O(圆心O在△ABC内部)经过B、C两点,交AB于点E,过点E作⊙O的切线交AC于点F.延长CO交AB于点G,作ED∥AC交CG于点D
(1)求证:四边形CDEF是平行四边形;
(2)若BC=3,tan∠DEF=2,求BG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
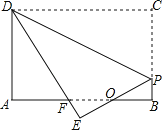
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC,AF⊥CD,垂足分别为E,F,且BE=DF.
(1)求证:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
(1)将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)判断以O,A1,B为顶点的三角形的形状.(无须说明理由)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com