
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点.以
的中点.以![]() 为直径作
为直径作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() 与
与![]() 相切于点
相切于点![]() .
.
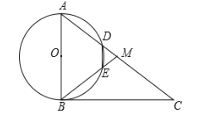
(1)求证:![]() ;
;
(2)若![]() ,
,![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半得AM=BM,进而得∠A=∠ABM,再根据圆内接四边形的性质得∠MDE=∠ABM,进而得∠A=∠MDE,据此可得答案.
(2)连接BD,由三角形面积求出BD,进而由勾股定理求得AD,再由△MDE∽△MAB求得DE.
解:(1)证明:∵BC与![]() 相切于点B,∴∠ABC=90°,
相切于点B,∴∠ABC=90°,
∵点M是AC的中点,∴BM=AM=CM,
∴∠MAB=∠MBA,
∵四边形ABED是![]() 的内接四边形,
的内接四边形,
∴∠ADE+∠ABE=180°,
∵∠MDE+∠ADE=180°,
∴∠MDE=∠ABE,
∴∠MDE=∠MAB.
∴DE∥AB.
(2)连接BD,如下图所示:
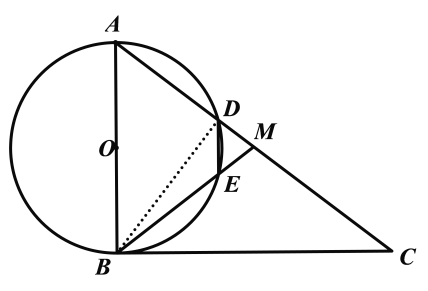
∵AB=6,BC=8,∠ABC=90°,
∴由勾股定理求得AC=10,
∵AB是![]() 的直径,
的直径,
∴∠ADB=90°,
∵AB×BC=AC×BD
∴![]() ,
,
∴![]() ,
,
∴DM=AM-AD=5-3.6=1.4,
∵DE∥AB,
∴△MDE∽△MAB,
∴![]() ,代入数据:
,代入数据:![]()
解得![]() .
.
故答案为:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市从一楼到二楼有一自动扶梯,如图是自动扶梯的侧面示意图,已知自动扶梯AB的坡度为1:2.4,AB的长度为13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处侧得C点的仰角为 42°,则二楼的层高BC约为(精确到0.1米,![]() ,
,![]() )( )
)( )
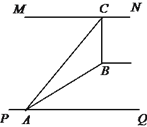
A.10.8米B.8.9米C.8.0米D.5.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
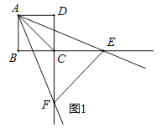
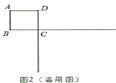
【题目】已知正方形![]() 的边长为4,一个以点
的边长为4,一个以点![]() 为顶点的
为顶点的![]() 角绕点
角绕点![]() 旋转,角的两边分别与边
旋转,角的两边分别与边![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,设
,设![]() .
.
(1)如图1,当![]() 被对角线
被对角线![]() 平分时,求
平分时,求![]() 的值;
的值;
(2)求证:![]() 与
与![]() 相似;
相似;
(3)当![]() 的外心在其边上时,求
的外心在其边上时,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
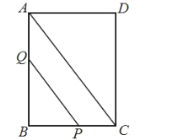
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上的一个动点、过点
边上的一个动点、过点![]() 作
作![]() 交
交![]() 边于点
边于点![]() ,把线段
,把线段![]() 绕点
绕点![]() 旋转至
旋转至![]() (点
(点![]() 与点
与点![]() 对应),点
对应),点![]() 落在线段
落在线段![]() 上,若
上,若![]() 恰好平分
恰好平分![]() ,则
,则![]() 的长为_________.
的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组的同学在研究函数![]() 的图象时,先对函数
的图象时,先对函数![]() 的图象进行了如下探索.
的图象进行了如下探索.
![]() ①列表:列出
①列表:列出![]() 与
与![]() 的几组对应值如下:
的几组对应值如下:
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
| ··· |
|
|
|
|
|
|
|
|
|
| ··· |
②描点:根据表中数据描点如图所示;
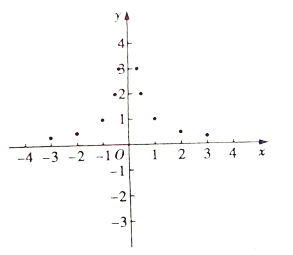
③连线:请在图中画出函数![]() 的图象;
的图象;
④观察图象,写出两条关于该函数的性质.
![]() 根据以上探究结果,完成下列问题:
根据以上探究结果,完成下列问题:
①函数![]() 中,自变量
中,自变量![]() 的取值范围为 ;
的取值范围为 ;
②函数![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
③写出两条关于函数![]() 的性质;
的性质;
④直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
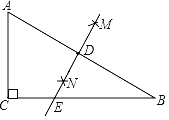
【题目】如图,在△ABC 中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于_____.
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上(不与A、B重合),∠ACB的平分线交AB于E,交⊙O于D,则下列结论不正确的是( )
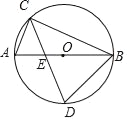
A. AB2=2BD2 B. ACBC=CECD
C. BD2=DEDC D. ACBC+BD2=AB2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com