
已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.当三角板绕点C旋转到CD与OA垂直时(如图1),易证得:OD+OE=![]() OC.当三角板绕点C旋转到CD与OA不垂直时:
OC.当三角板绕点C旋转到CD与OA不垂直时:
(1)在图2情况下上述结论仍成立,请给出证明;
(2)在图3情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.



图1 图2 图3
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源:2011届北京市海淀区初三一模数学试题 题型:解答题
已知:o为坐标原点,∠ AOB=300 , ∠ABO=900 且A(2,0)求: 过A、B、O三点的二次函数解析式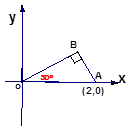
查看答案和解析>>
科目:初中数学 来源:2011-2012学年甘肃省天水市七年级上学期期末考试数学试卷(带解析) 题型:解答题
如图所示已知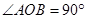 ,
,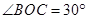 ,OM平分
,OM平分 ,ON平分
,ON平分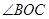 ;
;
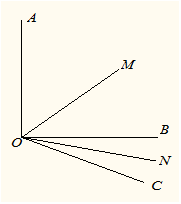
(1)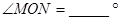 ;
; 
(2)如图∠AOB=900,将OC绕O点向下旋转,使∠BOC=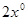 ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求出其值,若不能,试说明理由.
(3) 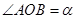 ,
,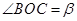 ,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求
,仍然分别作∠AOC,∠BOC的平分线OM,ON,能否求出∠MON的度数,若能,求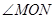 的度数;并从你的求解中看出什么什么规律吗?
的度数;并从你的求解中看出什么什么规律吗?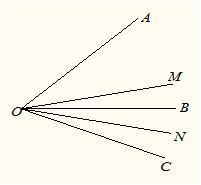
查看答案和解析>>
科目:初中数学 来源:2012年人教版初中数学九年级下26.1二次函数及其图像练习卷(解析版) 题型:解答题
已知:o为坐标原点,∠ AOB=300 , ∠ABO=900 且A(2,0)

求: 过A、B、O三点的二次函数解析式
查看答案和解析>>
科目:初中数学 来源: 题型:
已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.当三角板绕点C旋转到CD与OA垂直时(如图1),易证得:OD+OE=![]() OC.当三角板绕点C旋转到CD与OA不垂直时:
OC.当三角板绕点C旋转到CD与OA不垂直时:
(1)在图2情况下上述结论仍成立,请给出证明;
(2)在图3情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.



图1 图2 图3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com