
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

【答案】(1)证明见解析;(2)CG=![]() ;(3)∠EFC=120°或30°.
;(3)∠EFC=120°或30°.
【解析】分析: (1)作EP⊥CD于P,EQ⊥BC于Q,证明Rt△EQF≌Rt△EPD,得到EF=ED,根据正方形的判定定理证明即可;
(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解决问题.
(3)分两种情形考虑问题即可
详解:
(1)证明:作EP⊥CD于P,EQ⊥BC于Q,
∵∠DCA=∠BCA,
∴EQ=EP,
∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,
∴∠QEF=∠PED,
在Rt△EQF和Rt△EPD中,
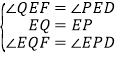 ,
,
∴Rt△EQF≌Rt△EPD,
∴EF=ED,
∴矩形DEFG是正方形;
(2)如图2中,在Rt△ABC中.AC=![]() AB=2
AB=2![]() ,
,
∵EC=![]() ,
,
∴AE=CE,
∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=![]() .
.

(3)①当DE与AD的夹角为30°时,∠EFC=120°,
②当DE与DC的夹角为30°时,∠EFC=30°
综上所述,∠EFC=120°或30°.
点睛: 本题考查正方形的性质、矩形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2017年李明家买了一辆轿车,他连续记录了一周中每天行驶的路程(如下表),以50km为标准,多于50km的记“+”,不足50km的记“-”,刚好506m的记“0”.
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 | |
路程(km) | -6 | 0 | -12 | 7 | -9 | +15 | +12 |
(1)请你求出李明家轿车一周中平均每天行驶多少千米?
(2)如果每行驶100km需要汽油8升,汽油价格6.85元/升,请计算李明家轿车一个月(按30天计算)的汽油费是多少元(精确到个位)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=(3-k)x-2k2+18.
(1)当k为何值时,它的图象经过原点?
(2)当k为何值时,它的图象经过点(0,-2)?
(3)当k为何值时,它的图象平行于直线y=-x?
(4)当k为何值时,y随x增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,O,B依次在直线MN上,如图1,现将射线OA绕点O顺时针方向以每秒10°的速度旋转,同时射线OB绕着点O按逆时针方向以每秒15°的速度旋转,直线MN保持不动,如图2,设旋转时间为t秒(t≤12).
(1)在旋转过程中,当t=2时,求∠AOB的度数.
(2)在旋转过程中,当∠AOB=105°时,求t的值.
(3)在旋转过程中,当OA或OB是某一个角(小于180°)的角平分线时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E,F.设CP=x,EF=y,则下列图象中,能表示y与x的函数关系的图象大致是( )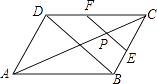
A.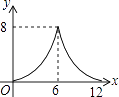
B.
C.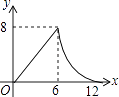
D.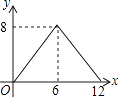
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P. 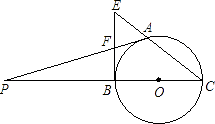
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+3+32+33+34+35+36+37+38的值时,张红发现:从第二个加数起每一个加数都是前一个加数的3倍,于是她假设:S=1+3+32+33+34+35+36+37+38 ①,然后在①式的两边都乘以3,得:3S=3+32+33+34+35+36+37+38+39 ②,
②一①得:3S―S=39-1,即2S=39-1,
∴S=![]() .
.
得出答案后,爱动脑筋的张红想:如果把“3”换成字母m(m≠0且m≠1),能否求出1+m+m2+m3+m4+…+m2016的值?如能求出,其正确答案是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1有两条长度相等的相交线段AB、CD,它们相交的锐角中有一个角为60°,为了探究AD、CB与CD(或AB)之间的关系,小亮进行了如下尝试:
(1)在其他条件不变的情况下使得AD∥BC,如图2,将线段AB沿AD方向平移AD的长度,得到线段DE,然后联结BE,进而利用所学知识得到AD、CB与CD(或AB)之间的关系: ;(直接写出结果)
(2)根据小亮的经验,请对图1的情况(AD与CB不平行)进行尝试,写出AD、CB与CD(或AB)之间的关系,并进行证明;
(3)综合(1)、(2)的证明结果,请写出完整的结论: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com