
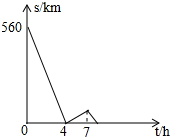
 一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:
一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后分别按原速同时驶往甲地,两车之间的距离S(km)与慢车行驶时间t(h)之间的函数图象如图所示,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据函数图象直接得出甲乙两地之间的距离;根据题意得出慢车往返分别用了4小时,慢车行驶4小时的距离,快车3小时即可行驶完,进而求出快车速度以及利用两车速度之比得出慢车速度;设慢车速度为3xkm/h,快车速度为4xkm/h,由(3x+4x)×4=560,可得x=20,从而得出快车的速度是80km/h,慢车的速度是60km/h.由题意可得出:快车和慢车相遇地离甲地的距离,当慢车行驶了7小时后,快车已到达甲地,可求出此时两车之间的距离即可.
解答 解:由题意可得出:甲乙两地之间的距离为560千米,故①正确;
由题意可得出:慢车和快车经过4个小时后相遇,出发后两车之间的距离开始增大直到快车到达甲地后两车之间的距离开始缩小,由图分析可知快车经过3个小时后到达甲地,此段路程慢车需要行驶4小时,因此慢车和快车的速度之比为3:4,故②错误;
∴设慢车速度为3xkm/h,快车速度为4xkm/h,
∴(3x+4x)×4=560,x=20
∴快车的速度是80km/h,慢车的速度是60km/h.
由题意可得出:快车和慢车相遇地离甲地的距离为4×60=240km,故④错误,
当慢车行驶了7小时后,快车已到达甲地,此时两车之间的距离为240-3×60=60km,故③正确.
故选:B.
点评 此题主要考查了待定系数法求一次函数解析式以及一次函数的应用,读懂图,获取正确信息是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | -12 | C. | 12或-12 | D. | 36 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
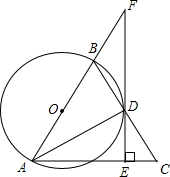 如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.
如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1250km | B. | 125km | C. | 12.5km | D. | 1.25km |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com