

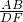 =
= ,
, =
= ,
,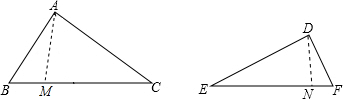
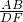 ≠
≠ ,
,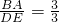 =1,
=1,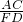 =
= =2.
=2.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| AB′ |
| AB |
| B′C′ |
| BC |
| AC′ |
| AC |
查看答案和解析>>
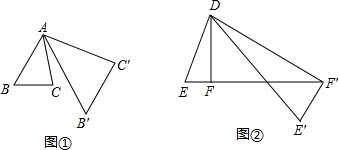
科目:初中数学 来源:2013届上海市虹口区中考二模数学试卷(带解析) 题型:填空题
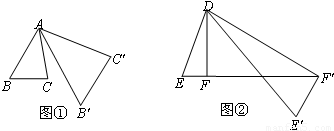
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍得△AB′ C′ ,即如图①,∠BAB′=θ, ,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .
,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .

查看答案和解析>>
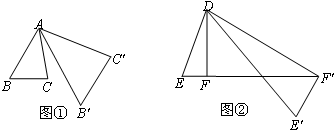
科目:初中数学 来源:2012-2013学年上海市虹口区中考二模数学试卷(解析版) 题型:填空题
将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍得△AB′ C′ ,即如图①,∠BAB′=θ, ,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .
,我们将这种变换记为[θ,n] .如图②,在△DEF中,∠DFE=90°,将△DEF绕点D旋转,作变换[60°,n]得△DE′F′,如果点E、F、F′恰好在同一直线上,那么n= .


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com