
 于点A、B,交抛物线C2:
于点A、B,交抛物线C2: 于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.
于点C、D.原点O关于直线AB的对称点为点Q,分别连接OA,OB,QC和QD.| m | 1 | 2 | 3 |
 | | | |
 = .请证明你的猜想.
= .请证明你的猜想.
| m | 1 | 2 | 3 |
 |  |  |  |
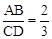 。理由见解析
。理由见解析 。
。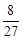 。
。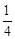 x2,1=
x2,1=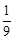 x2,∴x=±2,x=±3。∴AB=4,CD=6。∴
x2,∴x=±2,x=±3。∴AB=4,CD=6。∴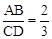 。
。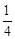 x2,4=
x2,4=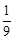 x2,∴x=±4,x=±6。∴AB=8,CD=12。∴
x2,∴x=±4,x=±6。∴AB=8,CD=12。∴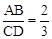 。
。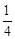 x2,9=
x2,9=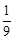 x2,∴x=±6,x=±9。∴AB=12,CD=18。∴
x2,∴x=±6,x=±9。∴AB=12,CD=18。∴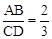 。
。| m | 1 | 2 | 3 |
 |  |  |  |
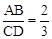 。证明如下:
。证明如下: ,得x=±2m,
,得x=±2m, ,得x=±3m,
,得x=±3m, 。
。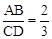 。
。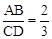 ,∴AB=
,∴AB= CD。
CD。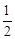 AB•PO,S△CQD=
AB•PO,S△CQD=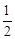 CD•PQ,∴
CD•PQ,∴ 。
。
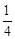 m4。∴4m2=m4,解得m1=0,m2=﹣2,m3=2。
m4。∴4m2=m4,解得m1=0,m2=﹣2,m3=2。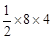 =16,S△CQD=
=16,S△CQD=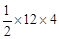 =24。
=24。
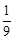 m4。∴9m2=m4,∴m1=0,m2=﹣3,m3=3。
m4。∴9m2=m4,∴m1=0,m2=﹣3,m3=3。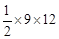 =54,S△CQD=
=54,S△CQD=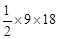 =81。
=81。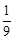 (﹣2m)2,y=
(﹣2m)2,y=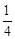 (3m)2,∴y=
(3m)2,∴y=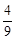 m2,y=
m2,y=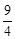 m2。∴E(﹣2m,
m2。∴E(﹣2m,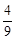 m2),F(3m,
m2),F(3m,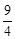 m2)。
m2)。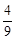 m2=
m2=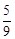 m2,DF=
m2,DF=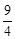 m2﹣m2=
m2﹣m2=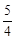 m2。
m2。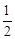 ×
×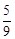 m2•2m=
m2•2m=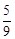 m3,S△DFM=
m3,S△DFM=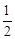 ×
×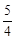 m2•3m=
m2•3m=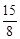 m3。∴
m3。∴ 。
。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:单选题

| A.这一天的温差是10℃ |
| B.在0:00--4:00时气温在逐渐下降 |
| C.在4:00--14:00时气温都在上升 |
| D.14:00时气温最高[ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
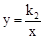 的图像没有公共点,则
的图像没有公共点,则| A.k1+k2<0 | B.k1+k2>0 | C.k1k2<0 | D.k1k2>0 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.3 | B.-1 | C.-3或1 | D.3或-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com