
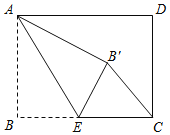
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将
,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处.当
处.当![]() 为直角三角形时,
为直角三角形时,![]() __.
__.
【答案】![]() 或5
或5
【解析】
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如图1所示.连结AC,先利用勾股定理计算出AC=13,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即ΔABE沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=5,可计算出CB′=8,设BE=a,则EB′=a,CE=12-a,然后在Rt△CEB′中运用勾股定理可计算出a.②当点B′落在AD边上时,如图2所示.此时ABEB′为正方形.
当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如图1所示,
连结AC,
在Rt△ABC中,AB=5,BC=12,
∴AC=![]() =13,
=13,
∵将ΔABE沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即将ΔABE沿AE折叠,使点B落在对角线AC上的点B′处,设:![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
由勾股定理得:![]() ,
,
解得:![]() ;
;
②当点B′落在AD边上时,如图2所示,
此时ABEB′为正方形,∴BE=AB=5,
综上所述,BE的长为![]() 或5,
或5,
故答案为:![]() 或5.
或5.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源: 题型:
【题目】为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了3.2米(BB‘),再把竹竿竖立在地面上,测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,PA、PB为⊙O的切线,M、N是PA、AB的中点,连接MN交⊙O点C,连接PC交⊙O于D,连接ND交PB于Q,求证:MNQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,观察数轴,请回答:
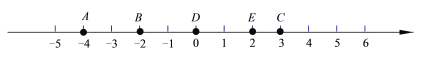
(1)点C与点D的距离为______ ,点B与点D的距离为______ ;
(2)点B与点E的距离为______ ,点A与点C的距离为______ ;
发现:在数轴上,如果点M与点N分别表示数m,n,则他们之间的距离可表示为 ______(用m,n表示)
(3)利用发现的结论解决下列问题: 数轴上表示x的点P与B之间的距离是1,则 x 的值是______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
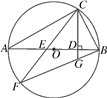
【题目】如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,过点C作直线CD⊥AB于点D,点E是AB上一点,直线CE交⊙O于点F,连接BF与直线CD延长线交于点G.求证:BC2=BG·BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.

(1)求证:四边形AODE是矩形;
(2)若AB=12,∠BCD=120°,求四边形AODE的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上对应的数为-2.
(1)点B在点A右边距离A点4个单位长度,则点B所对应的数是_____.
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒3个单位长度沿数轴向右运动.现两点同时运动,当点A运动到-6的点处时,求A、B两点间的距离.
(3)在(2)的条件下,现A点静止不动,B点以原速沿数轴向左运动,经过多长时间A、B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
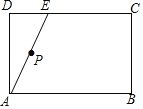
【题目】如图,矩形ABCD中,点E为矩形的边CD上的任意一点,点P为线段AE的中点,连接BP并延长与边AD交于点F,点M为边CD上的一点,且CM=DE,连接FM.
(1)依题意补全图形;
(2)求证∠DMF=∠ABF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com