Question

【题目】某市高中招生体育考试前教育部门为了解全市九年级男生考试项目的选择情况（每人限选一项），对全市部分九年级男生进行了调查，将调查结果分成五类：A、实心球（2kg）；B、立定跳远；C、50米跑；D、半场运球；E、其它．并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

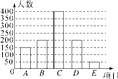
（1）将上面的条形统计图补充完整；

（2）假定全市九年级毕业学生中有5500名男生，试估计全市九年级男生中选“50米跑”的人数有多少人？

（3）甲、乙两名九年级男生在上述选择率较高的三个项目：B、立定跳远；C、50米跑；D、半场运球中各选一项，同时选择半场运球和立定跳远的概率是多少？请用列表法或画树形图的方法加以说明并列出所有等可能的结果．

Answer 1

【答案】（1）1000（2）2200（3）

【解析】试题分析：（1）用选择A的人数除以所占的百分比求出总人数，再乘以B所占的百分比求出B的人数，然后补全条形统计图即可；

（2）用5500乘以选50米跑所占的百分比，计算即可得解；

（3）画出树状图，然后根据概率公式列式即可得解．

试题解析：(1)被调查的学生总人数为150÷15%＝1000(人)，

选择B项目的人数为1000×(1－15%－20%－40%－5%)＝1000×20%＝200(人)，

补全统计图如图所示；

(2)5500×40%＝2200(人)，估计全市初三男生中选“50米跑”的人数有2200人；

(3)根据题意画出树状图如下：

所有等可能结果有9种：BB、BC、BD、CB、CC、CD、DB、DC、DD，同时选择B和D的有2种可能，即BD和DB，∴P(同时选择B和D)＝.