
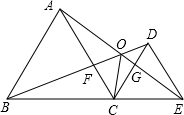
 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结OC、FG,则下列结论:①AE=BD;②AG=BF;③FG=CG;④∠BOC=∠EOC,⑤FG∥BE.其中结论正确的是①②③④⑤(只填序号)
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结OC、FG,则下列结论:①AE=BD;②AG=BF;③FG=CG;④∠BOC=∠EOC,⑤FG∥BE.其中结论正确的是①②③④⑤(只填序号) 分析 由等边三角形的性质得出AC=BC,CD=CE,∠ACB=∠DCE=60°,证出∠ACE=∠BCD,由SAS证明△AC≌△BCE,得出AE=BD,①正确;证出∠ACG=∠BCF=60°,由AAS证明△ACG≌△BCF,得出AG=BF,CG=CF,②正确;证出△CFG是等边三角形,得出FG=CG,∠FGC=∠GFC=60°=∠ACB,证出FG∥BE;③⑤正确;证明O、F、C、G四点共圆,由圆周角定理得出∠BOC=∠FGC=60°,∠COE=∠CFG=60°,得出∠BOC=∠EOC,④正确;即可得出结论.
解答 解: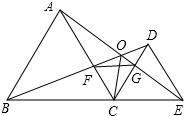 ∵△ABC和△CDE均是等边三角形,
∵△ABC和△CDE均是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠ACD=∠DCE+∠ACD,
即∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}&{\;}\\{∠ACE=∠BCD}&{\;}\\{CE=CD}&{\;}\end{array}\right.$,
∴△AC≌△BCE(SAS),
∴AE=BD,①正确;
∠CAG=∠CBF,
∵∠ACG=180°-2×60°=60°,
∴∠ACG=∠BCF=60°,
在△ACG和△BCF中,
$\left\{\begin{array}{l}{∠ACG=∠BCF}&{\;}\\{∠CAG=∠CBF}&{\;}\\{AC=BC}&{\;}\end{array}\right.$,
∴△ACG≌△BCF(AAS),
∴AG=BF,CG=CF,②正确;
∵∠ACG=60°,
∴△CFG是等边三角形,
∴FG=CG,∠FGC=∠GFC=60°=∠ACB,
∴FG∥BE;③⑤正确;
∵∠DOM=∠OBC+∠OEB=∠CAG+∠OEB=60°=∠FCG,
∴O、F、C、G四点共圆,
∴∠BOC=∠FGC=60°,∠COE=∠CFG=60°,
∴∠BOC=∠EOC,④正确;
结论正确的有①②③④⑤;
故答案为:①②③④⑤.
点评 本题考查了全等三角形的判定和性质,等边三角形的判定与性质,平行线的判定等知识;熟练掌握等边三角形的性质,证明三角形全等是解题的关键.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:解答题
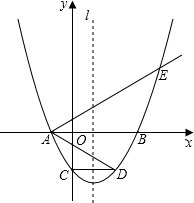 如图,已知二次函数y=m2x2-2mx-3(m是常数,m>0)的图象与x轴分别相交于点A、B(点A位于点B的左侧),与y轴交于点C,对称轴为直线l.点C关于l的对称点为D,连接AD.点E为该函数图象上一点,AB平分∠DAE.
如图,已知二次函数y=m2x2-2mx-3(m是常数,m>0)的图象与x轴分别相交于点A、B(点A位于点B的左侧),与y轴交于点C,对称轴为直线l.点C关于l的对称点为D,连接AD.点E为该函数图象上一点,AB平分∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x+y)(x-y) | B. | (x-1)(-1-x) | C. | (2x+y)(2y-x) | D. | (x-2)(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.6×10-7米 | B. | 6×10-8米 | C. | 6×10-9米 | D. | 6×10-7米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.3×10-5 | B. | 4.3×10-4 | C. | 4.3×10-6 | D. | 43×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
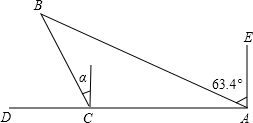 如图,一艘船在海面上由A向D方向航行,在相距4$\sqrt{5}$海里的A、C两地分别测得小岛B在A地的北偏西63.4°方向上,在C地的北偏西26.4°(α=26.4°)方向上,求C点与小岛B之间的距离BC(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin26.6°≈0.45,tan26.6°≈0.5,tan63.6°≈2).
如图,一艘船在海面上由A向D方向航行,在相距4$\sqrt{5}$海里的A、C两地分别测得小岛B在A地的北偏西63.4°方向上,在C地的北偏西26.4°(α=26.4°)方向上,求C点与小岛B之间的距离BC(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin26.6°≈0.45,tan26.6°≈0.5,tan63.6°≈2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com