
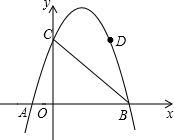
 与x轴交于点
与x轴交于点 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
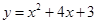 (2)①
(2)①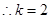 ∴对应函数的最小值是-3. ②∴点M的坐标是
∴对应函数的最小值是-3. ②∴点M的坐标是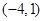 或
或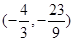
 ,得到关于b、c的二元一次方程组,解方程组求出b、c的值,关系式便可得出.(2)若抛物线向下平移k个单位,
,得到关于b、c的二元一次方程组,解方程组求出b、c的值,关系式便可得出.(2)若抛物线向下平移k个单位,
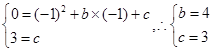
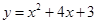
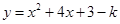
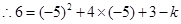 ;
;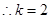
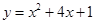
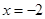 。
。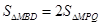
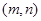 ,
,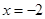 的左侧时,如图,则有
的左侧时,如图,则有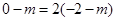 ,
,
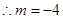 ,
,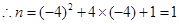 ,
,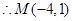 。
。 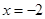 与y轴之间时,则有
与y轴之间时,则有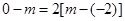
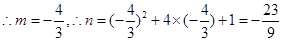 ,
,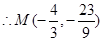
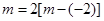
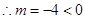 ,不合题意。
,不合题意。 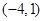 或
或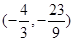


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.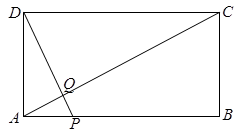
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
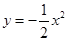 分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
分别相交于A、B两点.小明发现交点A、B两点的连线总经过一个固定点,则该点坐标为 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
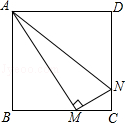
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com