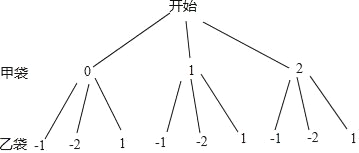
[题目] 在甲.乙两个不透明的布袋里.都装有3个大小.材质完全相同的小球.其中甲袋中的小球上分别标有数字0.1.2,乙袋中的小球上分别标有数字﹣1.﹣2.1．现从甲袋中任意摸出一个小球.记其标有的数字为x.再从乙袋中任意摸出一个小球.记其标有的数字为y.以此确定点M的坐标(x.y)．(1)请你用画树状图或列表的方法.写出点M所有可能的坐标,(2) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】在甲、乙两个不透明的布袋里，都装有3个大小、材质完全相同的小球，其中甲袋中的小球上分别标有数字0，1，2；乙袋中的小球上分别标有数字﹣1，﹣2，1．现从甲袋中任意摸出一个小球，记其标有的数字为x，再从乙袋中任意摸出一个小球，记其标有的数字为y，以此确定点M的坐标（x，y）．

（1）请你用画树状图或列表的方法，写出点M所有可能的坐标；

（2）求点M（x，y）落在函数y＝﹣的图象上的概率．

【答案】（1）点M所有可能的坐标为：（0，﹣1），（0，﹣2），（0，1），（1，﹣1），（1，﹣2），（1，1），（2，﹣1），（2，﹣2），（2，1）；（2）点M（x，y）落在函数y＝﹣的图象上的概率为．

【解析】

（1）根据题意画树状图即可得到结论；
（2）根据M（x，y）在函数y=-的图象上的有（-1，1），于是得到结论．

（1）画树状图得，则点M所有可能的坐标为：（0，﹣1），（0，﹣2），（0，1），（1，﹣1），（1，﹣2），（1，1），（2，﹣1），（2，﹣2），（2，1）；

（2）∵M（x，y）在函数y＝﹣的图象上的有（1，﹣1），

∴点M（x，y）落在函数y＝﹣的图象上的概率为：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】广州火车南站广场计划在广场内种植A，B两种花木共 6600棵，若A花木数量是B花木数量的2倍少600棵．

（1）A，B两种花木的数量分别是多少棵？

（2）如果园林处安排26人同时种植这两种花木，每人每天能种植A花木60棵或B花木40棵，应分别安排多少人种植A花木和B花木，才能确保同时完成各自的任务？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在△ABC中，∠ACB=90°，∠ACB与∠CAB的平分线交于点P，PD⊥AB于点D，若△APC与△APD的周长差为，四边形BCPD的周长为12+，则BC等于______．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】在平面直角坐标系xOy中，抛物线经过点，．

求该抛物线的函数表达式及对称轴；

设点B关于原点的对称点为C，点D是抛物线对称轴上一动点，记抛物线在A，B之间的部分为图象包含A，B两点，如果直线CD与图象G有两个公共点，结合函数的图象，直接写出点D纵坐标t的取值范围．

查看答案和解析>>

科目：初中数学 来源： 题型：

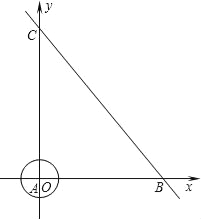
【题目】如图，在直角坐标系中，半径为1的⊙A圆心与原点O重合，直线l分别交x轴、y轴于点B、C，点B的坐标为（6，0），∠ABC＝60°．

（1）若点P是⊙A上的动点，则P到直线BC的最小距离是　　．

（2）若点A从原点O出发，以1个单位/秒的速度沿着线路OB→BC→CO运动，回到点O停止运动，⊙A随着点A的运动而移动．设点A运动的时间为t．

①求⊙A在整个运动过程中与坐标轴相切时t的取值；

②求⊙A在整个运动过程中所扫过的图形的面积．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图坐标系中，O(0，0) ，A(6，6)，B(12，0)．将△OAB沿直线CD折叠，使点A恰好落在线段OB上的点E处，若OE＝，则CE : DE的值是______．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，Rt△ABC中，M为斜边AB上一点，且MB=MC=AC=8cm，平行于BC的直线l从BC的位置出发以每秒1cm的速度向上平移，运动到经过点M时停止. 直线l分别交线段MB、MC、AC于点D、E、P，以DE为边向下作等边△DEF，设△DEF与△MBC重叠部分的面积为S（cm2），直线l的运动时间为t（秒）．