Question

13．如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE=∠BAD，AE⊥AC，DA平分∠BDE．
（1）求证：四边形ABDE是菱形；
（2）如果AB=5，AD=6，求四边形ABDE的面积．

Answer 1

分析 （1）通过BD垂直AC，AE⊥AC，说明AE∥BD，通过∠ADE=∠BAD，说明AB∥ED，从而说明四边形ABDE是平行四边形，再有DA平分∠BDE，说明AE=ED，所以平行四边形ABDE是菱形．
（2）过点E作AD的高线，求出高长，计算出△AED的面积，再计算出菱形ABDE的面积．

解答 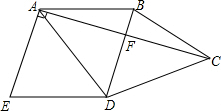（1）证明：∵BD垂直平分AC，
∴∠CFD=90°，
∵AE⊥AC，
∴∠EAC=90°，
∴∠CFD=∠EAC
∴AE∥BD
∵∠ADE=∠BAD，
∴AB∥ED，
∴四边形ABDE是平行四边形
∵DA平分∠BDE，
∴∠BAD=∠EAD．
∵∠ADE=∠BAD，
∴∠EAD=∠ADE，
∴AE=ED
∴四边形ABDE是菱形．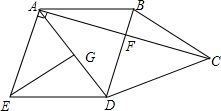
（2）解：过点E作EG⊥AD，
∵AE=ED，
∴AG=GD=3，
又∵ED=AB=5，
∴在RT△EDG中，EG=4
∴S_△AED=$\frac{1}{2}$AD•EG=$\frac{1}{2}$×6×4=12．
∴S_{四边形ABDE}=2S_△AED=2×12=24．

点评 本题考查了平行四边形、菱形的判定和三角形的面积．菱形的一条对角线把菱形分成两个全等的三角形，两条对角线把菱形分成四个全等的直角三角形，菱形的面积=$\frac{1}{2}$边×该边上的高=$\frac{1}{2}$×两条对角线的积．