
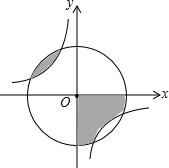
 如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )
如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{k}$ | D. | $\frac{1}{π}$ |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
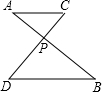 如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )
如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )| A. | ∠APD=39° | B. | ∠APD=50° | C. | ∠APD=89° | D. | ∠APD=76° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若x=y,则x-m=y-m | B. | 若x=y,则mx=my | C. | 若$\frac{x}{m}$=$\frac{y}{m}$,则x=y | D. | 若x=y,则$\frac{x}{m}$=$\frac{y}{m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
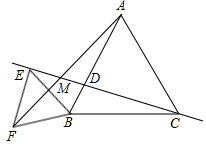 如图,等边△ABC中,点D是AB上一点,点E在线段CD延长线上,以BE为一边且在BE的左侧作等边△BEF,连接AF.
如图,等边△ABC中,点D是AB上一点,点E在线段CD延长线上,以BE为一边且在BE的左侧作等边△BEF,连接AF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
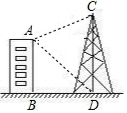 如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )
如图,已知楼房AB高50m,铁塔塔基距楼房基间的水平距离BD=50m,塔高DC为$\frac{1}{3}$(150+50$\sqrt{3}$)m,下列结论中,正确的是( )| A. | 由楼顶望塔基俯角为60° | B. | 由楼顶望塔顶仰角为60° | ||
| C. | 由楼顶望塔基俯角为30° | D. | 由楼顶望塔顶仰角为30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com