
【题目】如图坐标系中,O(0,0),A(6,6![]() ),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=
),B(12,0),将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,若OE=![]() ,则AC:AD的值是( )
,则AC:AD的值是( )
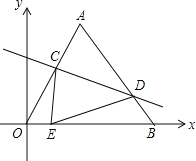
A.1:2B.2:3C.6:7D.7:8
【答案】B
【解析】
过A作AF⊥OB于F,根据已知条件得到△AOB是等边三角形,推出△CEO∽△EDB,根据相似三角形的性质得到![]() ,求出BE=OB﹣OE=12﹣
,求出BE=OB﹣OE=12﹣![]() =
=![]() ,设CE=a,则CA=a,CO=12﹣a,ED=b,则AD=b,DB=12﹣b,于是得到12b=60a﹣5ab,48a=60b﹣5ab,两式相减得到48a﹣12b=60b﹣60a,即可得到结论.
,设CE=a,则CA=a,CO=12﹣a,ED=b,则AD=b,DB=12﹣b,于是得到12b=60a﹣5ab,48a=60b﹣5ab,两式相减得到48a﹣12b=60b﹣60a,即可得到结论.
解:过A作AF⊥OB于F,如图所示:
∵A(6,![]() ),B(12,0),
),B(12,0),
∴AF=![]() ,OF=6,OB=12,
,OF=6,OB=12,
∴BF=6,
∴OF=BF,
∴AO=AB,
∵tan∠AOB=![]() =
=![]() ,
,
∴∠AOB=60°,
∴△AOB是等边三角形,
∴∠AOB=∠ABO=60°,
∵将△OAB沿直线CD折叠,使点A恰好落在线段OB上的点E处,
∴∠CED=∠OAB=60°,
∴∠OCE=∠DEB,
∴△CEO∽△EDB,
∴![]() ,
,
∵OE=![]() ,
,
∴BE=OB﹣OE=12﹣![]() =
=![]() ,
,
设CE=a,则CA=a,CO=12﹣a,ED=b,则AD=b,DB=12﹣b,
则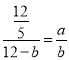 ,
,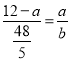 ,
,
∴12b=60a﹣5ab①,48a=60b﹣5ab②,
②﹣①得:48a﹣12b=60b﹣60a,
∴![]() ,即AC:AD=2:3.
,即AC:AD=2:3.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D为AC中点,E为AB上的动点,将ED绕点D逆时针旋转90°得到FD,连CF,则线段CF的最小值为_____.
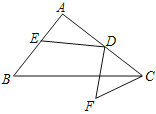
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,篮球1个,若从中任意摸出一个球,摸到球是红球的概率为![]() .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,求两次摸到球的颜色是红色与黄色这种组合(不考虑红、黄球顺序)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种贺卡原售价每张1元,甲商店这种贺卡七折优惠,而在乙商店这种贺卡除了八折优惠外,购买30张以上(含30张)免费送5张. 设一次买这种贺卡x张(x是正整数且30≤x≤50),若选择在甲商店购买需用y1元,若选择在乙商店购买需用y2元.
(1)假定你代购买45张这种贺卡,请确定应在哪一个商店买花钱较少;
(2)请分别写出y1(元)与x(张)、y2(元)与x(张)之间的函数关系式;
(3)在x的取值范围内,试讨论在哪一个商店买花钱较少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC≌△DEC,公共顶点为C,B在DE上,则有结论①∠ACD=∠BCE=∠ABD;②∠DAC+∠DBC=180°;③△ADC∽△BEC;④CD⊥AB,其中成立的是( )
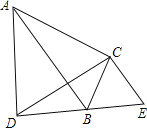
A.①②③B.只有②④C.只有①和②D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,抛物线y=﹣x2+4x+m﹣4(m为常数)与y轴的交点为C,M(3,0)与N(0,﹣2)分别是x轴、y轴上的点
(1)当m=1时,求抛物线顶点坐标.
(2)若3≤x≤3+m时,函数y=﹣x2+4x+m﹣4有最小值﹣7,求m的值.
(3)若抛物线与线段MN有公共点,直接写出m的取值范围是 .
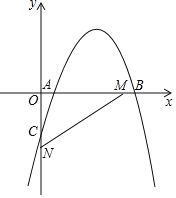
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解答问题.
材料:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线例如:如图①,AD把△ABC分成△ABD与△ADC,若△ABD是等腰三角形,且△ADC∽△BAC,那么AD就是△ABC的完美分割线.
解答下列问题:
(1)如图②,在△ABC中,∠B=40°,AD是△ABC的完美分割线,且△ABD是以AD为底边的等腰三角形,则∠CAD= 度.
(2)在△ABC中,∠B=42°,AD是△ABC的完美分割线,且△ABD是等腰三角形,求∠BAC的度数.
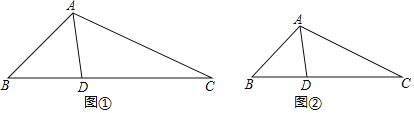
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD
(1) 求证:E是OB的中点
(2) 若AB=8,求CD的长

查看答案和解析>>
科目:初中数学 来源: 题型:
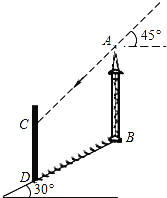
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com