
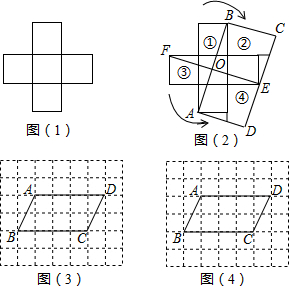
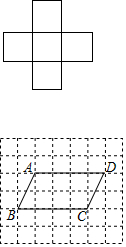
分析 (1)如图3中,取AD中点H,沿CH剪开,①旋转到②的位置即可(△HCD绕点H逆时针旋转180°即可);
(2)在BC上取一点E,使得CE=1,沿AE、ED剪开,①放到②的位置,③放到④的位置即可;
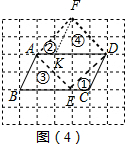
解答 解:(1)如图3中,取AD中点H,沿CH剪开,①旋转到②的位置即可(△HCD绕点H逆时针旋转180°即可),
△EBC即为等腰三角形(EB=EC=2$\sqrt{5}$).
(2)在BC上取一点E,使得CE=1,沿AE、ED剪开,①放到②的位置,③放到④的位置即可,
正方形AEDF即为所求.
点评 本题考查四边形综合题、复杂作图、等腰三角形的性质、正方形的判定和性质等知识,解题的关键是利用数形结合的思想解决问题,本题考查了学生的动手能力,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
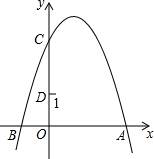 如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).
如图,抛物线y=-x2+2x+3与y轴交于点C,点D(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,则点P的坐标为(1+$\sqrt{2}$,2)或(1-$\sqrt{2}$,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
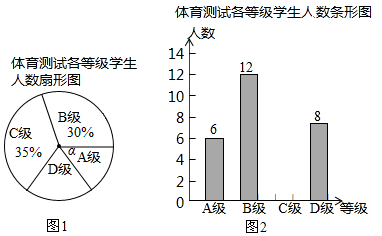
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
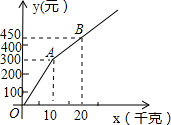 甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
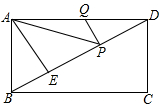 如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.
如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE=$\frac{\sqrt{3}}{3}$,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
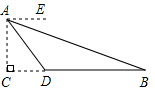 为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)
为了测量校园池塘B,D两地之间的距离,从距离地面高度为20米的教学楼A处测得点B的俯角∠EAB=15°,点D的俯角∠EAD为45°,点C在线段BD的延长线上,AC⊥BC,垂足为C,求池塘B,D两地之间的距离(结果保留整数米).(参考数据:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com