练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】新型冠状病毒肺炎疫情发生后，全社会积极参与疫情防控工作，某市为了尽快完成100万只口罩的生产任务，安排甲、乙两个大型工厂完成．已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍，并且在独立完成60万只口罩的生产任务时，甲厂比乙厂少用5天，求甲、乙两厂每天能生产口罩多少万只？

    【答案】甲厂每天能生产口罩6万只，乙厂每天能生产口罩4万只.

    【解析】

    先由题意得出等量关系：甲厂每天能生产口罩的数量=乙厂每天能生产口罩的数量×1.5，工作时间=工作总量÷工作效率，乙厂独立完成60万所用天数-甲厂独立完成60万所用天数=5，然后设未知数代入相关数据即可解答．

    解：设乙厂每天能生产口罩x万只，则甲厂每天能生产口罩1.5x万只，

    依题意，得： ，

    解得：x＝4，

    经检验，x＝4是原方程的解，且符合题意，∴1.5x＝6．

    答：甲厂每天能生产口罩6万只，乙厂每天能生产口罩4万只．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（本题10分）如图，在平面直角坐标系xOy中，直线与y轴交于点C，与x轴交于点B，抛物线经过B、C两点，与x轴的正半轴交于另一点A，且OA ：OC="2" ：7．

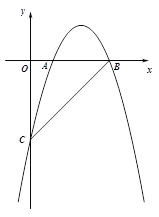
    （1）求抛物线的解析式；

    （2）点D为线段CB上，点P在对称轴的右侧抛物线上，PD=PB，当tan∠PDB＝２，求P点的坐标；

    （3）在（2）的条件下，点Q（7，m）在第四象限内，点R在对称轴的右侧抛物线上，若以点P、D、Q、R为顶点的四边形为平行四边形，求点Q、R的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

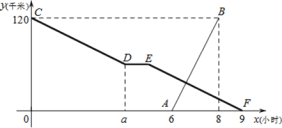
    【题目】甲、乙两地相距 120 千米，小张骑自行车从甲地出发匀速驶往乙地，出发 a小时开始休息，1 小时后仍按原速继续行驶．小李比小张晚出发一段时间，骑摩托车从乙地匀速驶往甲地，图中折线 CD－DE－EF，线段 AB 分别表示小张、小李与乙地的距离 y（千米）与小张出发时间 x（小时）之间的函数关系图象．

    （1）小李到达甲地后，再经过 小时小张到达乙地；小张骑自行车的速度是 千米/时；

    （2）当 a＝4 时，求小张与乙地的距离 y乙 与小张出发的时间 x（小时）之间的函数关系式；

    （3）若小张恰好在休息期间与小李相遇，请直接写出 a 的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

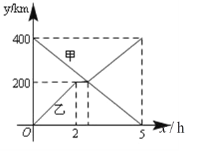
    【题目】甲，乙两辆汽车分别从A，B两地同时出发，沿同一条公路相向而行，乙车出发2h后休息，与甲车相遇后，继续行驶．设甲，乙两车与B地的路程分别为y甲(km)，y乙 (km)，行驶的时间为x(h)，y甲，y乙与x之间的函数图象如图所示，结合图象解答下列问题：

    （1）乙车休息了多长时间；

    （2）求乙车与甲车相遇后y乙与x的函数解析式，并写出自变量x的取值范围；

    （3）当两车相距40km时，求出x的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

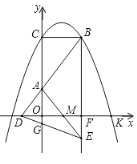
    【题目】如图，与轴交于点C，与轴的正半轴交于点K，过点作轴交抛物线于另一点B，点在轴的负半轴上，连结交轴于点A，若．

    （1）用含的代数式表示的长；

    （2）当时，判断点是否落在抛物线上，并说明理由；

    （3）过点作轴交轴于点延长至，使得连结交轴于点连结AE交轴于点若的面积与的面积之比为则求出抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

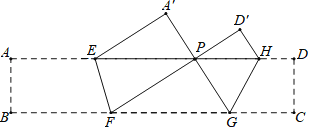
    【题目】如图，把某矩形纸片ABCD沿EF，GH折叠（点E，H在AD边上，点F，G在BC边上），使点B和点C落在AD边上同一点P处，A点的对称点为A′点，D点的对称点为D′点，若∠FPG＝90°，△A′EP的面积为8，△D′PH的面积为2，则矩形ABCD的面积等于 （ ）

    A.B.C.D.16＋12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

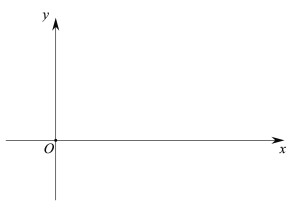
    【题目】如图，平面直角坐标系，抛物线（，）与轴交于A、B两点（A在B左侧），与轴交于点C，过抛物线的顶点P且与轴平行的直线交BC于点D，且满足BD：CD=3：2，

    （1）若∠ACB=90°，求抛物线解析式；

    （2）问OC和DP能否相等？若能，求出抛物线解析式，若不能，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

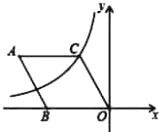
    【题目】如图，在菱形ABOC中，AB＝2，∠A＝60°，菱形的一个顶点C在反比例函数y＝（k≠0）的图象上，则反比例函数的解析式为（ ）

    A.y＝B.y＝C.y＝D.y＝

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2020年3月至5月，某校开展了一系列居家阅读活动．学生利用“宅家”时光，在书海中遨游，从阅读中获得精神慰藉和自我提升．为了解学生居家阅读的情况，学校从七、八两个年级各随机抽取50名学生，进行了居家阅读情况调查．下面给出了部分数据信息：

    ．两个年级学生平均每周阅读时长（单位：小时）的频数分布直方图如下（数据分成4组：，，，）：

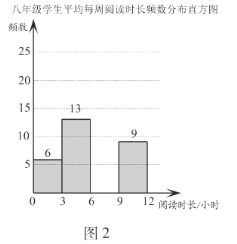
    b．七年级学生平均每周阅读时长在这一组的是：6 6 7 7 7 7 7 8 8 8 8 8 8 8 8 8

    c．两个年级学生平均每周阅读时长的平均数、中位数、众数、方差如下：

    平均数

    中位数

    众数

    方差

    七年级

    6.3

    8

    7.0

    八年级

    6.0

    7

    7

    6.3

    根据以上信息，回答下列问题：

    （1）补全图2；

    （2）写出表中的值；

    （3）返校后，学校计划将平均每周阅读时长不低于9小时的学生授予“阅读之星”称号．小丽说：“根据频数分布直方图中的数据信息，估计七年级约有20%的学生获得该称号，八年级约有18%的学生获得该称号，所以七年级获得该称号的人数一定比八年级获得该称号的人数多．”你认为她的说法________（填入“正确”或“错误”）；

    （4）请你结合数据对两个年级的居家阅读情况进行评价．

    查看答案和解析>>

    同步练习册答案