
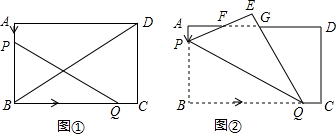
分析 (1)由运动得出BP=BQ,求出t,即可;
(2)由PM∥AD,得出$\frac{PM}{AD}=\frac{BP}{AB}$,表示出PM,从而求出t,即可;
(3)先判断出△AEP≌△FEG,表示出BH,HQ,CQ,再由勾股定理计算即可.
解答 解:(1)当BP=BQ时,60-3t=20t,
∴t=$\frac{60}{23}$,
故答案为:$\frac{60}{23}$;
(2)如图1,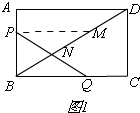 过P作PM∥AD,
过P作PM∥AD,
∴$\frac{PM}{AD}=\frac{BP}{AB}$,
∴$\frac{PM}{90}=\frac{60-3t}{60}$,
∴PM=90-$\frac{9}{2}$t,
∵PN=NQ,PM=BQ,
∴90-$\frac{9}{2}$t=20t,
∴t=$\frac{180}{49}$;
(3)如图2,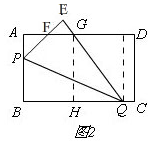 作GH⊥BQ于H,
作GH⊥BQ于H,
∴PB=PF=60-3t,
∵AE=EF,∠AEP=∠FEG,∠A=∠F,
∴△AEP≌△FEG,
∴PE=EG,FG=AP,
∴AG=PF=60-3t=BH,
∴HQ=BQ-BH=20t-(60-3t)=23t-60,
GQ=FQ-FG=BQ-AP=17t,
根据勾股定理得,602=(17t)2-(23t-60)2
∴t1=4,t2=7.5(舍),
∴t=4
∴存在t=4,使AE=EF.
点评 此题是四边形综合题,主要考查了矩形的性质,等腰三角形的性质,平行线分线段成比例定理,全等三角形的性质和判定,勾股定理等知识;本题综合性强,有一定难度,用时间t表示线段是解本题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
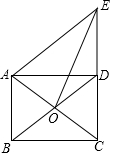 如图,矩形ABCD的对角线AC,BD相交于点O,过点A作BD的平行线交CD的延长线于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,过点A作BD的平行线交CD的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com