
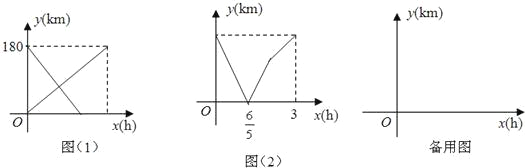
【题目】甲、乙两车分别从A、B两地同时相向而行,匀速开往对方所在地,图(1)表示甲、乙两车离A地的路程y(km)与出发时间x(h)的函数图象,图(2)表示甲、乙两车间的路程y(km)与出发时间x(h)的函数图象.
(1)A、B两地的距离为 km,![]() h的实际意义是 ;
h的实际意义是 ;
(2)求甲、乙两车离B地的路程y(km)与出发时间x(h)的函数关系式及x的取值范围,并画出图象(不用列表,图象画在备用图中);
(3)丙车在乙车出发10分钟时从B地出发,匀速行驶,且比乙车提前20分钟到达A地,那么,丙车追上乙车多长时间后与甲车相遇?
【答案】(1)180;![]() h时甲乙两车相距0km;(2)l甲:y=-60x+180(0≤x≤3)l乙:y=90x(0≤x≤2).(3)丙车追上乙车
h时甲乙两车相距0km;(2)l甲:y=-60x+180(0≤x≤3)l乙:y=90x(0≤x≤2).(3)丙车追上乙车![]() h后与甲车相遇.
h后与甲车相遇.
【解析】
试题分析:(1)从图(1)可看出甲乙路程相距180km,从图(2)可看出![]() h他们相距0km,故这个时间相遇.
h他们相距0km,故这个时间相遇.
(2)从图中根据时间和路程可求出甲和乙的速度,设l甲:y=k1x+180,l乙:y=k2x,从而求出函数式.画出函数图象.
(3)设l丙:y=k3x+b,由题意知l丙经过(![]() ,0),(
,0),(![]() ,180),从而确定函数式找到它与甲的交点,从而求出解.
,180),从而确定函数式找到它与甲的交点,从而求出解.
试题解析:(1)180,甲、乙两车出发![]() h两车相遇.
h两车相遇.
(2)由题意,v甲=![]()
![]() (v甲+v乙)=180,
(v甲+v乙)=180,
即v乙=90
∴乙车从B地到达A地所用的时间为![]()
由题意,设l甲:y=k1x+180,l乙:y=k2x
则3k1+180=0,即k1=-60,
∴l甲:y=-60x+180(0≤x≤3)
2k2=180,即k2=90,
∴l乙:y=90x(0≤x≤2).
(画出图象)

(3)设l丙:y=k3x+b,由题意知l丙经过(![]() ,0),(
,0),(![]() ,180)
,180)
∴ 即
即
∴l丙:y=120x-20.
![]() ∴
∴![]()
![]() ∴
∴![]()
∴![]() ,即丙车追上乙车
,即丙车追上乙车![]() h后与甲车相遇.
h后与甲车相遇.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】已知点A(x1,y1),B(x2,y2)在二次函数y=-x2-2x的图象上.若x1>x2>-1,则y1____y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了进一步开展“阳光体育”活动,计划用2000元购买乒乓球拍,用2800元购买羽毛球拍.已知一副羽毛球拍比一副乒乓球拍贵14元.该校购买的乒乓球拍与羽毛球拍的数量能相同吗?
(1)根据题意,甲和乙两同学都先假设该校购买的乒乓球拍与羽毛球拍的数量能相同,并分别列出的方程如下:甲:![]() ;乙:
;乙:![]() ,根据两位同学所列的方程,请你分别指出未知数x,y表示的意义:
,根据两位同学所列的方程,请你分别指出未知数x,y表示的意义:
甲:x表示 ;乙:y表示 ;
(2)该校购买的乒乓球拍与羽毛球拍的数量能相同吗?说明理由(写出完整的解答过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 过一点有且只有一条直线与已知直线垂直
B. 三角形任意两边之和小于第三边
C. 三角形的一个外角大于它的任何一个内角
D. 平行与同一条直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家教育部规定“中小学生每天在校体育活动时间不低于1小时”.某中学为了解学生体育活动情况,随机抽查了520名毕业班学生,调查内容是:“每天锻炼是否超过1小时及未超过1小时的原因”,并根据调查结果绘制成如下不完整的统计图.
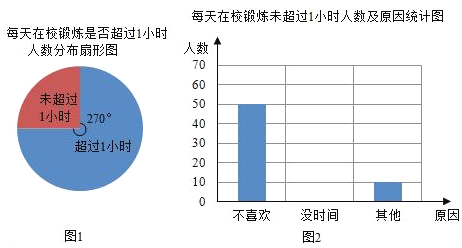
根据统计图提供的信息,解答下列问题:
(1)这520名毕业生中每天在校锻炼时间超过1消失的人数是 .
(2)请补全条形统计图.
(3)2016年该中学所在城市的初中毕业生约为5.2万人,估计2016年该城市初中毕业生中因为没时间导致每天锻炼时间未超过1小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列一元二次方程中,没有实数根的是( )
A. 4x2﹣5x+2=0 B. x2﹣6x+9=0 C. 5x2﹣4x﹣1=0 D. 3x2﹣4x+1=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com