
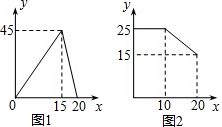
分析 (1)分两种情况进行讨论:①0≤x≤15;②15<x≤20;针对每一种情况,都可以先设出函数的解析式,再将已知点的坐标代入,利用待定系数法求解;①0≤x<10时p=25,10≤x≤20时,设解析式为p=mx+n,利用待定系数法求解;
(2)日销售金额=日销售单价×日销售量.日销售量不低于36千克,即y≥36.先解不等式3x≥36,得x≥12,再解不等式-9x+180≥36,得x≤16,则求出“最佳销售期”共有4天;然后根据x的范围分类讨论,利用二次函数的性质,即可解答.
解答 解:(1)分两种情况:
①当0≤x≤15时,设日销售量y与销售时间x的函数解析式为y=k1x,
∵直线y=k1x过点(15,45),
∴15k1=45,解得k1=3,
∴y=3x(0≤x≤15);
②当15<x≤20时,设日销售量y与销售时间x的函数解析式为y=k2x+b,
∵点(15,45),(20,0)在y=k2x+b的图象上,
∴$\left\{\begin{array}{l}{15{k}_{2}+b=45}\\{20{k}_{2}+b=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{2}=-9}\\{b=180}\end{array}\right.$
∴y=-9x+180(15<x≤20);
综上,可知y与x之间的函数关系式为:y=$\left\{\begin{array}{l}{3x}&{(0≤x≤15)}\\{-9x+180}&{(15<x≤20)}\end{array}\right.$.
①当0≤x<10时,p=25,
当10≤x≤20时,设销售单价p(元/千克)与销售时间x(天)之间的函数解析式为p=mx+n,
∵点(10,25),(20,15)在p=mx+n的图象上,
∴$\left\{\begin{array}{l}{10m+n=25}\\{20m+n=15}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-1}\\{n=35}\end{array}\right.$,
∴p=-x+35(10≤x≤20),
∴p=$\left\{\begin{array}{l}{25}&{(0≤x<10)}\\{-x+35}&{(10≤x≤20)}\end{array}\right.$;
(2)若日销售量不低于36千克,则y≥36.
当0≤x≤15时,y=3x,
解不等式:3x≥36,
得,x≥12;
当15<x≤20时,y=-9x+180,
解不等式:-9x+180≥36,
得x≤16,
∴12≤x≤16,
∴“最佳销售期”共有:16-12+1=5(天);
当12≤x≤15时,销售额W=3x(-x+35)=-3(x-$\frac{35}{2}$)2+$\frac{3675}{4}$,
∴当x=15时,W取得最大值,最大值为900;
当15≤x≤16时,销售额W=(-9x+180)(-x+35)=9(x-$\frac{55}{2}$)2-506.25,
∴当x=15时,W取得最大值,最大值为900,
综上,第15天的销售额最大,
答:此次销售过程中“最佳销售期”共有5天,在此期间销售金额最高是第15天.
点评 此题考查了一次函数的应用,有一定难度.解题的关键是理解题意,利用待定系数法求得函数解析式,注意数形结合思想与函数思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
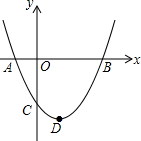 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1,3.与y轴负半轴交于点C,在下面五个结论中:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com