
分析 (1)根据得(3分),即为黑球、白球各1个,画出树状图,分求得甲取得3分的概率和乙取得3分的概率;
(2)根据乙取得3分的概率小于$\frac{1}{20}$,则$\frac{2}{n+1}$<$\frac{1}{20}$,进而得到n>39,据此可得白球的数量.
解答 解:(1)得(3分),即为黑球、白球各1个,
甲从暗箱中有放回地依次取出2只球,画树状图: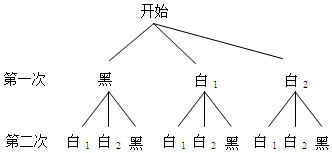
∴甲取得(3分)的概率$\frac{4}{9}$,
乙是从暗箱中一次性取出2只球.画树状图: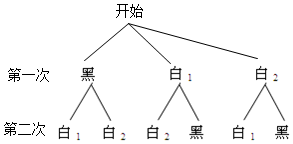
∴甲取得(3分)的概率=$\frac{4}{6}$=$\frac{2}{3}$;
(2)若乙取得3分的概率小于$\frac{1}{20}$,则$\frac{2}{n+1}$<$\frac{1}{20}$,
∴n>39,
∴白球至少有40个.
点评 本题主要考查了利用列表法或树状图法计算概率,当有两个元素时,可用树形图列举,也可以列表列举.解题时注意:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{10000}{x}$-10=$\frac{14700}{(1+40%)x}$ | B. | $\frac{10000}{x}$+10=$\frac{14700}{(1+40%)x}$ | ||
| C. | $\frac{10000}{(1-40%)x}$-10=$\frac{14700}{x}$ | D. | $\frac{10000}{(1-40%)x}$+10=$\frac{14700}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
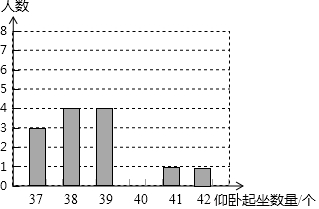 某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题
某校为了解本校九年级女生“仰卧起坐”的训练情况,随机抽查了该年级m名女生进行测试,并按测试成绩绘制出以下两幅不完整的统计表,请根据图中的信息解答下列问题| 测试成绩(个) | 学生数(名) | 百分比 |
| 37 | 3 | P% |
| 38 | 4 | 20% |
| 39 | 4 | 20% |
| 40 | N | 35% |
| 41 | 1 | 5% |
| 42 | 1 | 5% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.
为了发展乡村旅游,建设美丽从化,某中学七年级一班同学都积极参加了植树活动,今年四月份该班同学的植树情况部分如图所示,且植树2株的人数占32%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
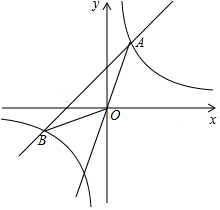 如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.
如图,直线y=4x与反比例函数y=$\frac{k}{x}$(k≠0)相交与点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,且tanα=$\frac{1}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
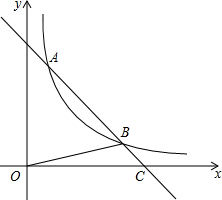 如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.
如图,直线y1=-mx+5m与双曲线y2=$\frac{k}{x}$(x>0)相交于A、B(4,n)两点,与x轴相交于C点,△BOC的面积是$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间段(小时/周) | 小丽抽样(人数) | 小杰抽样(人数) |
| 0~1 | 6 | 22 |
| 1~2 | 10 | 10 |
| 2~3 | 16 | 6 |
| 3~4 | 8 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
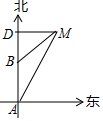 如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).
如图所示,轮船由A处以每小时28海里的速度向正北方向航行,此时测得灯塔M在北偏东30°的方向上(即∠BAM=30°).半小时后,轮船航行到B处,此时测得灯塔M在北偏东60°的方向(即∠DBM=60°).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com