
【题目】学习了三角形全等的判定方法(即SSS,SAS,ASA,AAS)和直角三角形全等的判定方法(即HL)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
(初步思考)
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后对∠B进行分类,可以分为“∠B是直角、钝角、锐角”三种情况进行探究.
(深入探究)
第一种情况:当∠B为锐角时,△ABC和△DEF不一定全等.
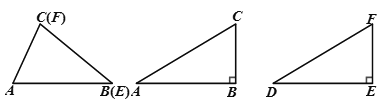
(1)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你用尺规在图中确定点D,使△DEF和△ABC不全等(不写作法,保留作图痕迹);
第二种情况:当∠B为直角时,△ABC≌△DEF.
(2)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据____,可以知道Rt△ABC≌Rt△DEF.
第三种情况:当∠B为钝角时,△ABC≌△DEF.
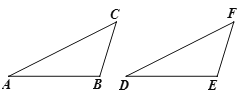
(3)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,求证:△ABC≌△DEF.
【答案】(1)图见解析;(2)HL;(3)证明见解析
【解析】
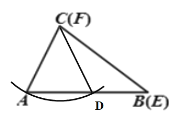
(1)以点C为圆心,AC的长度为半径画弧,与AB的交点为点D,连接CD即可得出;
(2)根据题目条件可利用HL证明Rt△ABC≌Rt△DEF;
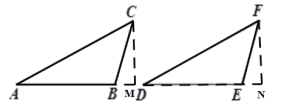
(3) 过点C作CM⊥AB的延长线于M,过点F作FN⊥DE的延长线于N,先证得△CBM≌△FEN,再证明△ACM≌△DFN,最后可得到△ABC≌△DEF.
解:(1)如图所示:
 ;
;
(2)在Rt△ABC和Rt△DEF中,
![]() ,
,
∴Rt△ABC≌Rt△DEF(HL),
故答案为:HL;
(3)证明:过点C作CM⊥AB的延长线于M,过点F作FN⊥DE的延长线于N,
∵∠ABC=∠DEF,
∴∠CBM=∠FEN,
在△CBM和△FEN中,
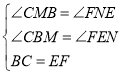 ,
,
∴△CBM≌△FEN,
∴CM=FN,BM=EN,
在Rt△ACM和Rt△DFN中,
![]() ,
,
∴Rt△ACM≌Rt△DFN(HL),
∴AM=DN,
∴DE=AB,
在△ABC和△DFE中,
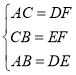 ,
,
∴△ABC≌△DEF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
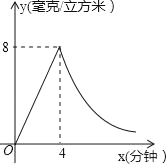
【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,AC=2AB,AD平分∠BAC交BC于点D,延长DB至点F,使BF=BD连接AF.
(1)求证:AF=CD.
(2)若CE平分∠ACB交AB于点E,试猜想AC,AF,AE三条线段之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线C1:![]() 与x轴的一个交点为A(-1,0),另一个交点为B,与
与x轴的一个交点为A(-1,0),另一个交点为B,与![]() 轴的交点为C(0,-3),其顶点为D.
轴的交点为C(0,-3),其顶点为D.
(1)求抛物线C1的解析式;
(2)如图1,将△OBC沿![]() 轴向右平移m个单位长度(0﹤
轴向右平移m个单位长度(0﹤![]() ≤
≤![]() )得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
)得到另一个三角形△EFG,将△EFG与△BCD重叠部分(四边形BPGQ)的面积记为S,用含m的代数式表示S;
(3)如图2,将抛物线C1平移,使其顶点为原点O,得到抛物线C2.若直线![]() 与抛物线C2交于S、T两点,点
与抛物线C2交于S、T两点,点![]() 是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.
是线段ST上一动点(不与S、T重合),试探究抛物线C2上是否存在一点R,点R关于点N的中心对称点K也在抛物线C2上.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足,下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=EF=EC;④BA+BC=2BF,其中正确的结论有________(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com