练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．某市2016年有3000名学生参加初中毕业生会考，要想了解这3000名学生的数学成绩，从中随机抽取了300名学生的数学成绩进行统计分析，在此问题汇总，总体是3000名学生的数学成绩，样本是随机抽取了300名学生的数学成绩．

    分析 总体是指考查的对象的全体，个体是总体中的每一个考查的对象，样本是总体中所抽取的一部分个体，而样本容量则是指样本中个体的数目．我们在区分总体、个体、样本、样本容量，这四个概念时，首先找出考查的对象．从而找出总体、个体．再根据被收集数据的这一部分对象找出样本，最后再根据样本确定出样本容量．

    解答 解：某市2016年有3000名学生参加初中毕业生会考，要想了解这3000名学生的数学成绩，从中随机抽取了300名学生的数学成绩进行统计分析，在此问题汇总，总体是3000名学生的数学成绩，样本是随机抽取了300名学生的数学成绩，
    故答案为：3000名学生的数学成绩，随机抽取了300名学生的数学成绩．．

    点评 考查了总体、个体、样本、样本容量，解题要分清具体问题中的总体、个体与样本，关键是明确考查的对象．总体、个体与样本的考查对象是相同的，所不同的是范围的大小．样本容量是样本中包含的个体的数目，不能带单位．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．（1）计算：（-1）2016+2sin60°-|-$\sqrt{3}$|+π0．
    （2）先化简，再求值：$\frac{x}{{x}^{2}-1}$•$\frac{{x}^{2}+x}{{x}^{2}}$，其中x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．有相距3个单位的两点A（a，-3），B（2，b），且AB平行于坐标轴，求a、b．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

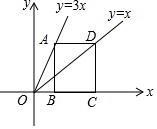    9．如图，点A、D分别在两条直线y=3x和y=x上，AD∥x轴，已知B、C都在x轴上，且四边形ABCD是矩形，则$\frac{AD}{AB}$的值是（　　）
    A．$\frac{1}{3}$B．$\frac{2}{3}$C．3D．$\frac{3}{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．对于正数x，用符号[x]表示x的整数部分，例如：[0.1]=0，[2.5]=2，[3]=3．点A（a，b）在第一象限内，以A为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直．其中垂直于y轴的边长为a，垂直于x轴的边长为[b]+1，那么，把这个矩形覆盖的区域叫做点A的矩形域．例如：点$（3，\frac{3}{2}）$的矩形域是一个以$（3，\frac{3}{2}）$为对角线交点，长为3，宽为2的矩形所覆盖的区域，如图1所示，它的面积是6．

    根据上面的定义，回答下列问题：
    （1）在图2所示的坐标系中画出点$（2，\frac{7}{2}）$的矩形域，该矩形域的面积是8；
    （2）点$P（2，\frac{7}{2}），Q（a，\frac{7}{2}）（a＞0）$的矩形域重叠部分面积为1，求a的值；
    （3）已知点B（m，n）（m＞0）在直线y=x+1上，且点B的矩形域的面积S满足4＜S＜5，那么m的取值范围是$\frac{4}{3}$＜m＜$\frac{5}{3}$．（直接写出结果）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．已知某市2017年企业用水量x（吨）与该月应交的水费y（元）之间的函数关系如图所示．
    （1）当0≤x≤50时，求y关于x的函数关系式；
    （2）当50≤x≤60时，求y关于x的函数关系式；
    （3）若某企业3月份用水量为40吨，求该企业3月份应交的水费；
    （4）若某企业5月份用水量为620吨，求该企业在5月份的用水量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．计算：4$\sqrt{5}$+$\sqrt{45}$-10$\sqrt{\frac{1}{5}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）计算：（1-$\sqrt{3}$）2（1-$\sqrt{2}$）2（1+$\sqrt{2}$）2（1+$\sqrt{3}$）2-（$\sqrt{3}$-$\sqrt{2}$）2
    （2）用适当方法解方程．x2-2x=2x+1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

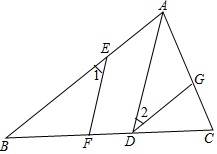    11．已知：如图，点D、E、G分别是△ABC边BC、AB和AC上的点，AD∥EF，点F在BC上，∠1=∠2=∠B．
    求证：①AB∥DG；②DG平分∠ADC．

    查看答案和解析>>

    同步练习册答案